§6  代数数

    [代数数]  若q 为一系数为有理数的代数方程

的根,则q 称为代数数.通分后,q满足一有理整*系数的代数方程,因此代数数也可定义为“有理整系数的代数方程的根”.

    若f(x)为有理数域上不可约多项式,且,则q 称为n次代数数.显然,一次代数数为有理数.

    代数数具有下列性质:

    1°  两个代数数的和、差、积、商(除数非零)仍为代数数.

    2°  系数为代数数的代数方程的根仍为代数数.

    [代数整数]  若q 为一首项系数为1,其他系数为有理整数的n次不可约代数方程的根,则q 称为n次代数整数.

    代数整数具有下列性质:

    1°  代数整数为有理数的(即一次代数整数)必为有理整数.

    2°  两个代数整数的和、差、积仍为代数整数.

    3°  首项系数为1,其他系数为代数整数的代数方程的根仍为代数整数.

    4°  若q 为代数数,即满足有理整系数方程

则 为代数整数.

    5°  若q 为n次代数整数,则q 的幂可表为

式中i为非负整数,都为有理整数.

    6°  若q 为n次代数数,则q 的幂满足等式

式中i为非负整数,为有理整数.

    [单位数]  若q 与都为代数整数,则q 称为单位数.

    单位数具有下列性质:

    1°  q 为单位数的充分必要条件是:q 为首项系数为1,常数项为的有理整系数代数方程的根.

    2°  首项系数和常数项都为单位数,其他系数为代数整数的代数方程的根为单位数.

    [代数扩域]

    1°  单扩域  设q 为n次代数数,则形为

 (系数为有理数)

的数的全体构成一个域.称为在有理数域Q上添加q所得的n次单扩域,记作Q(q ).若,则Q(q )为由代数数q 经加、减、乘、除(除数非零)所生成的数的最大集合.

    2°  有限扩域  由有限多个代数数经加、减、乘、除(除数非零)所生成的域,称为Q上的有限扩域,记作

K=Q()

    有限扩域必为单扩域,即存在代数数q ,使得

Q()=Q(q )

q的次数称为有限扩域Q()的次数.

    [共轭数]  设q 为n次代数数,q满足有理数域上n次不可约多项式  

记,又设为该多项式的另外n－1个根,则称为q的共轭根.

    任意代数数a Q(q ),则a可唯一地表为

                                 (1)

式中为有理数.记,则

          

称为a 的共轭数.

    [代数数的迹与矩]  设a K=Q(q ),记,设是a 的共轭数,则分别称

为代数数a 的迹与矩,式中如(1)式定义.

    注意,这里的迹与矩是对域K而言的,矩又称为范数.它们的另一个定义是：设a 的极小多项式(以a 为根的最低次不可约多次式)为      

    令,则

    迹与矩具有下列性质:

    1°  若a 为代数数,则a的迹与矩均为有理数.

    2° 若a 为代数整数, 则a 的迹与矩为有理整数.若a 为非零代数整数,则.

    3°  代数整数a 为单位数的充分必要条件是:.

    4°                      S(a+b )=S(a )+S(b )

                                     N(ab ) =N(a )N(b )

    [代数数域的基底与整底]

    1°  基底  设K为n次代数扩域,为K中一组代数数,若K中任意代数数g都可唯一地表为

式中为有理数,则称为K的一组基底.显然在有理数域上线性无关.

    是域K的一组基底的充分必要条件是:

式中是的共轭数, j=.

    若K=Q(q ),则为K的一组基底.

    2°  整底  设K为n次代数扩域,为K中一组代数整数,若K中任意代数整数g 都可唯一地表为

式中为有理整数,则称为K的一组整底.

    若为一组使

为最小的代数整数,则这组为一组整底.

    [二次域]  设D为一无平方因子的有理整数.则Q()为二次域.Q()中的任意代数数都可表为

式中a和b都为有理数.

    设D为一无平方因子的有理整数.

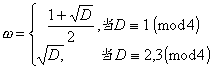
则1,w 为二次域Q()的一组整底.

    一般n次域Q不一定能找到代数整数w,使

构成Q(q )的一组整底.

    [高斯域]  设,则Q(i)称为高斯域,它是二次域.

    高斯域中的任意数可表为

式中a,b都为有理数.当a,b都为有理整数时,a+bi称为高斯整数.

    高斯域有四个单位数:,它们的矩都为1.

    [分圆域]  设m为正整数,把多项式的所有根添加到Q上所构成的域S称为Q上的m次单位根的分圆域.

    S中存在一个m次本原单位根q (q 是的根,但不是的根(n<m),称q为m次本原单位根),使得S=Q(q ),而构成S的一组整底.

    如果q是m次本原单位根,使也是m次本原单位根,共有(m)个,这里(m)为欧拉函数.

    [分解定理]

    1°  整除性  若a ,b 为二代数整数,当仍为代数整数时,则称b 可整除a ,记作.这时称a 是b 的倍数,b 是a 的因数.

    2°  结合性  若二代数整数a ,b 仅相差一单位数因子,则称a 与b 是相结合的.

    显然有:  (i)  a 与a 相结合; (ii)  若a 与b 相结合,则b 与a 相结合; (iii)  若a 与b 相结合,b 与g 相结合,则a 与g 相结合.

    3°  不可分解  若K中的代数整数a ,有另外两个代数整数b ,g K,且都不是单位数,使

a =bg

则称a 在域K中可分解,否则称为不可分解.

    4°  分解定理  在K中的任意一代数整数可以分解为不可分解的代数整数的乘积.

    如果不计次序和结合性,这种分解是唯一的,则称为唯一分解.

    高斯域的唯一分解定理成立.

    二次域中唯一分解定理成立的,现已知道有

Q(),  D=2,3,5,6,7,13,17,21,29等.

   不是所有的二次域唯一分解定理都成立,例如Q()唯一分解定理不成立: