§5 多项式
[整值多项式] 当变数x为整数时,一多项式f(x)的值常为整数，则这种多项式称为整值多项式。
整系数多项式是整值多项式一特例。
整值多项式表达式：
1° 凡n次整值多项式必可表为
式中
为整数，
2° 整值奇多项式(满足f(－x)=－f(x))必可表为
式中
为整数.
3° 整值偶多项式(满足f(－x)=f(x)) 必可表为
式中
为整数.
[可约多项式与不可约多项式] 设f(x)为一有理系数多项式,若有非常数的有理系数多项式g(x)和h(x),使得
f(x)=g(x)h(x)
则称f(x)为在有理数域上可约(或可化),否则称f(x)为有理数域上的不可约多项式(简称不可约多项式).
[高斯定理] 设f(x)为一整系数多项式,在有理数域上可约,则必有二整系数多项式g(x)和h(x),使得
f(x)=g(x)h(x)
[爱森斯坦判别法]
1° 设
为一整系数多项式.若有素数p,使得
但 
则f(x)为不可约多项式.
2° 设
为2n+1次整系数多项式,若有素数p,使得
但 
则f(x)为不可约多项式.
[派朗判别法]
1° 设
为一首项系数为1的n次整系数多项式,满足条件:
(i)
(i)
(ii)
(ii)
(iii) 
实数)
则f(x)为不可约多项式.
2° 设
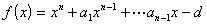
为一首项系数为1的n次整系数多项式,满足条件:
(i) 
(ii) 
则f(x)为不可约多项式.
3° 设
为一首项系数为1的n次整系数多项式,满足条件:
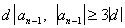
则f(x)为不可约多项式.
4° 设
为一首项系数为1的n次整系数多项式,满足条件:
则f(x)为不可约多项式.
5° 设
为一首项系数为1,常数项不为零的n次整系数多项式,满足条件:
则f(x)为不可约多项式.
[多项式的整除性] 设f(x)和g(x)为二有理系数多项式,g(x)不恒为零,若有一多项式h(x),使得
f(x)=g(x)h(x)
则称g(x)可整除f(x),记作
或 
这时g(x)称为f(x)的因式,f(x)称为g(x)的倍式.否则,g(x)不能整除f(x),记作
.
以下¶°f表示多项式f(x)的次数.
多项式的整除性具有下列性质:
1° 
2° 若
且
,则f与g仅相差一常数因子.
3° 若
,
则
4° 若
,则¶°f
¶°g
若
,而
,则f称为g的真因式,显然¶°f<¶°g.
5° 若p(x)为一不可约多项式,且
,则
或
.
6° 若p(x)为一不可约多项式,且
f(x)=0,p(x)=0
有公共根,则必有
.
[多项式的带余除法] 设f(x),g(x)为任意多项式,g(x)不恒为零,则必有两个多项式q(x)和r(x),使得
f(x)=g(x)q(x)+r(x)
式中r(x)=0或¶°r<¶°g.这称为多项式的带余除法.
[多项式的辗转相除法] 多项式的辗转相除法与整数的辗转相除法的定义,公式完全类似,只须把本章§1(1)式中的文字符号看作多项式就行了.
同样,多项式的唯一分解定理,最高公因式和最低公倍式,多项式互素等概念和公式与整数一节完全类似,只须把相应公式中的符号看作多项式就行了.
例 求多项式
与
的最高公因式.
解 为了避免分数,先用2乘f(x),然后再用g(x)去除2f(x):
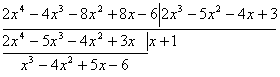
在计算过程中,用2乘第一个差,因而商式变了样,但余式
只获得一个数因子2,这不关紧要.用3乘g(x),除以
:
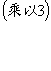
可取
所以所求的公因式为
.
[同余式]
1° 多项式模同余式 设m(x)为一多项式,若
则称f(x)与g(x)对模m(x)同余,记作
2° 素数模同余式 设p为素数,f(x)与g(x)为整系数多项式,若各项对应系数都对模p同余,则称此二多项式对模p同余,记作
3° 重模同余式 设p为素数,
(x)为多项式,若f(x)－g(x)为
(x)的倍式,mod p,则称f(x)与g(x)对重模p, 
(x)同余,记作
f(x)
g(x) 
[费马定理的推广]
设p为素数, 
(x)为n次不可约多项式,mod p,则对任一非
(x)的倍式的多项式f(x),mod p,恒有
1 
对任一多项式常有
f(x) 
特别
x 