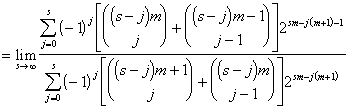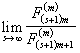§2 连分数
[简单连分数] 设a 为实数(有理数或无理数),则可表成简单连分数
(2)
简记为 ![]()
或 ![]()
式中![]() 为整数,
为整数,![]() 为正整数.
为正整数.
若a 为有理数![]() ,则必可展成有限连分数
,则必可展成有限连分数
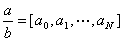
式中![]() 是由辗转相除法一列等式(1)所得到的一列不完全商.如果规定最后一个不完全商大于1,即当
是由辗转相除法一列等式(1)所得到的一列不完全商.如果规定最后一个不完全商大于1,即当![]() 时,可写成
时,可写成
![]()
则表法唯一.
若a 为无理数,则可展成无限连分数,且表法唯一.
[完全商与不完全商]
简单连分数(2)中![]() 称为a 的第i个不完全商.数
称为a 的第i个不完全商.数![]() 称为a 的第n个完全商.显然
称为a 的第n个完全商.显然![]() .
.
完全商与不完全商的关系:
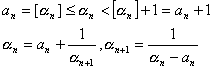
(n=0,1,2,…)
式中![]() 为a的第n个渐近分数的分子和分母(见下).
为a的第n个渐近分数的分子和分母(见下).
[渐近分数与最佳渐近分数] 简单连分数(1)中截取
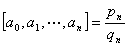
称为a 的第n个渐近分数.渐近分数都为既约分数.
1° 渐近分数的等式与不等式
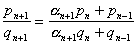
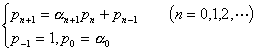
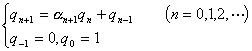
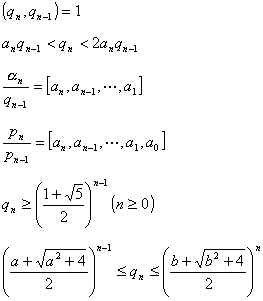
(当时)
(当a为实二次无理数时)
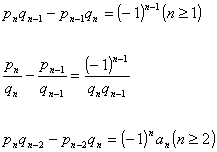
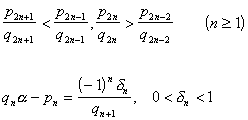
(式中![]() 为n的递减函数。a 为有理数时,此式仅当
为n的递减函数。a 为有理数时,此式仅当![]() 时成立,
时成立,![]() )
)
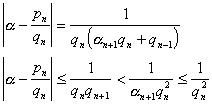
2° 设![]() 且
且![]() 则
则
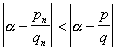
因此在分母不大于![]() 的所有分数中,
的所有分数中,![]() 与a 最接近(称
与a 最接近(称![]() 为最佳渐近分数).
为最佳渐近分数).
3° a 的两个相邻渐近分数中必有一个![]() 适合于
适合于
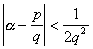
4° a 的三个相邻渐近分数中必有一个![]() 适合于
适合于
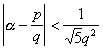
5° 设a 为实数,![]() 为有理数,M为正整数.若a 适合于不等式
为有理数,M为正整数.若a 适合于不等式
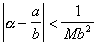
则a 展成连分数的不完全商至少有一个大于M-2.
[周期连分数及其充分必要条件]
当![]() 时,若
时,若![]() ,则连分数
,则连分数
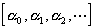
称为以k为周期的周期连分数,记做
(3)
当l=0时,(3)式称为纯周期连分数,当l=1时,(3)式称为拟纯周期连分数.
1° 实数a 可展成周期连分数的充分必要条件是:a是一个有理数域上二次不可约多项式的根.
2° 实二次无理数a 可展成纯周期连分数的充分必要条件是:a >1且![]() ,这里a’为a 的共轭实数.
,这里a’为a 的共轭实数.
3° 实二次无理数a 可展成拟纯周期连分数的充分必要条件是:a’<[a]-1,这里a’为a 的共轭实数, [a ]为a 的整数部分.
[![]() ,e与p 的连分数]
,e与p 的连分数]
1° 设![]() 为非完全平方数,则
为非完全平方数,则
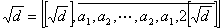
2° 设e为自然对数的底,则
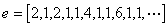
式中不完全商的通式为
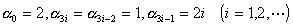
3° 设p为圆周率,则
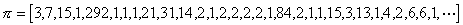
它的渐近分数为
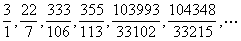
[二次域Q(![]() )的整底的连分数表]
)的整底的连分数表]
|
w |
连分数表示 |
w |
连分数表示 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[4,7] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[黄金分割与费波那奇序列]
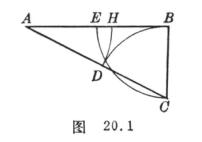
1° 把线段AB分成中外比(即![]() )的分割称为黄金分割.也就是求解代数方程
)的分割称为黄金分割.也就是求解代数方程
|
|
![]()
的一个根
![]()
黄金分割的几何作图见图20.1(E为AB中点).
2° 由递推关系
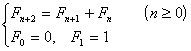
产生的序列

称为费波那奇序列.其通项表达式为
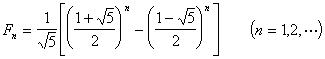
3° 当![]() 时,
时,![]() .
.
4° ![]() 是
是![]() 的最佳渐近分数,
的最佳渐近分数,![]() 是
是![]() 的最佳渐近分数.
的最佳渐近分数.
5° 设a,b为自然数,由递推关系
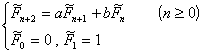
产生的序列的通项表达式为
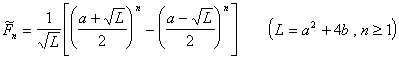
并且具有性质: 当![]() 时,
时,![]() .
.
[推广的费波那奇序列] 由递推关系
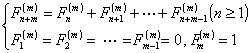
产生的序列称为m级推广的费波那奇序列.其通项表达式为
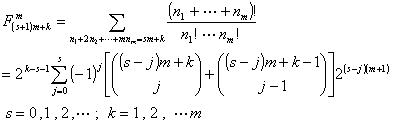 *
*
设w 为方程
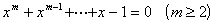
的唯一正实根,则
w=