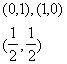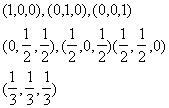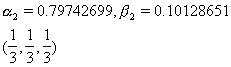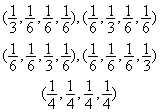附录   有限元法中的数值积分

在单元分析中需要计算大量数值积分，这些积分常常通过坐标变换把被积函数（包括对整体直角坐标的微分算子矩阵B)全部化为局部坐标的函数，并且其中大部分是关于局部坐标的多项式。对于方块剖分，它可化为坐标变量x，h，z的幂函数的积分，对于三角剖分，它可化为自然坐标的幂函数的积分，它们都不难求积。下面列出有关公式。对于被积函数不是多项式的积分，则需用高斯型求积公式求其近似值。关于局部坐标（x，h，z）的函数的数值积分可参看第六章，这里仅列出关于自然坐标的函数的高斯型数值积分表。

[线段单元]

1°    1°     含距离坐标的积分公式

由于，结合上式，可得出包含的积分公式。

2°    2°     常用的数值积分表

求积节点个数m	求积节点坐标	求积系数	代数精确度*n
1		1	1
2	(α,1),(1,α) 其中α=0.2113248654		3
3			3
3	(α,1),(1,α) 其中α=0.1127016654		5

[三边形单元]

1°    1°      含面积坐标的积分公式

式中A为单元的面积。从系数矩阵的积分公式（2）看出，被积函数不仅包含面积坐标为变量的型函数，而且也有关于x,y的微分算子B.根据矩阵坐标变换

再结合上式可得出包含的积分公式。

注意，如三边形单元任意一边（例如）作为线元，则上述含距离坐标的积分公式也成立。

2°    2°       常用的数值积分表

求积节点个数m	求积节点坐标	求积系数	代数精确度n
1		1	1
3			2
7			3
7	其中 其中	0.13239415 0.12593918 0.225	5

[四面体单元]

1°    1°       含体积坐标的积分公式

式中V为单元的体积。公式（2）出现，即被积函数包含型函数关于x,y,z的导数，根据坐标变换

                                                    (i=1,2,3)

再结合上式，可得出包含这些偏导数的积分公式

2°    2°     常用的数值积分表

求积节点个数m	求积节点坐标	求积系数	代数精确度n
1		1	1
4	其中		2
5			3