六、  六、        六面体单元

    [三向距离坐标]   设六面体的顶点为(i=1,2,…,8)(图19.5)。利用双向距离坐标,先把四边形变换到局部坐标系(ξ,η,ζ)的坐标面ζ=0上的单位正方形(0≤ξ≤1,0≤η≤1);再在线段上定义距离坐标,并取作(1-ζ,ζ), 的ζ分别为0与1。现在又对四边形利用双向距离坐标,把它变换到坐标面ζ=1上的单位正方形(0≤ξ≤1,0≤η≤1)。这就在四边形与分别同ζ=0与ζ=1上的单位正方形各点间建立一一对应。最后把上下四边形具同样局部坐标(ξ,η)的点联成线段,并沿方向(由下而上)定义距离坐标(1-ζ,ζ)。于是该线段上任意一点P的局部坐标可取为(ξ,η,ζ)。这样,直角坐标系中的任意六面体单元与局部坐标系中的单位立方体(0≤ξ≤1,0≤η≤1,0≤ζ≤1)之间就建立了一一对应。

[型函数]    对于单位立方体，利用节点的对称性得出型函数为

     

        

            

                           

由于顶点的局部坐标取值为1或0,可统一写成

（i=1,2,…,8）

它是三线性的,即对ξ或η或ζ都是线性的。

[坐标变换及其雅可比式]

  

同一样,它是三线性的。这表明六面体的棱边应是直线段。

雅可比式（即变换矩阵的行列式）为

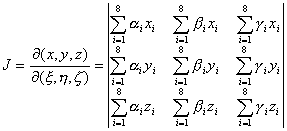
式中

变换矩阵也可写成

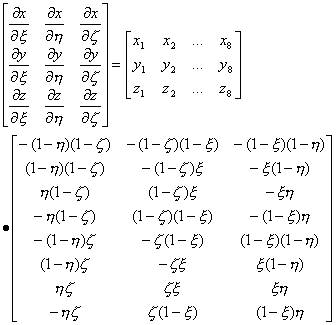
从上式看出变换矩阵各行关于ξ,η,ζ的二次项系数是相同的,记

对也有相应的记号,则变换矩阵可写成

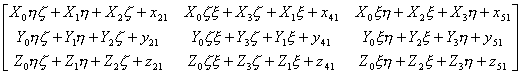
其行列式是ξ,η,ζ的四次多项式,而且各项的系数为零。

[三线性插值函数]