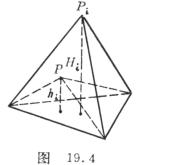
五、四面体单元

[体积坐标]  设四面体顶点为(i=1,2,3,4),则四面体的任一点P的体积坐标定义为

      (i=1,2,3,4)

式中表示P与所对的底面三角形构成四面体的体积,V为四面体单元的体积,而分别表示P,到底面的距离。显然,的体积坐标除外,其余且有

                         (12)

[型函数]    就是体积坐标(i=1,2,3,4),它们与直角坐标之间的线性关系式为

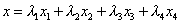
                              (13)

[坐标变换及其雅可比式]   假定为独立变量,则由上(12),(13)得

         

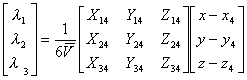
式中

，，             

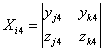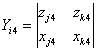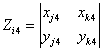
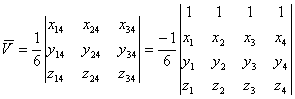
其绝对值等于单元体积V即。

雅可比式（即变换矩阵的行列式）为

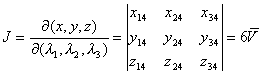
逆变换矩阵为

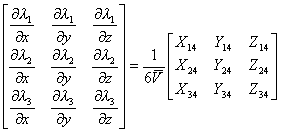
 [线性插值函数]

 

由(12),(13)可直接求得

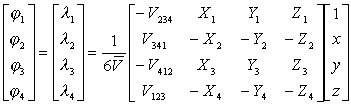
等式右端系数矩阵各元素可循环定义如下：

     

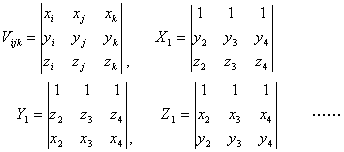
实际上不难看出，,…，只不过这里用三阶行列式代替X_i4等二阶行列式，便于循环定义,结果还是一致的。