§6 最小（大）值原理
[连续系统的最小（大）值原理] 考虑一控制系统其状态方程为
(1)
并满足初始条件
(2)
至于终止状态
则或者是自由的，或者是满足目标集
(3)
性能指标为
(4)
式中x和m分别是状态矢量和控制矢量：
是n维矢函数，R是m维矢函数。
假设
,
,G(x,t),R(x,t)都是其变元的连续函数，对x连续可微，并且
有界。
假设控制矢量m(t)是容许控制，即满足下列条件：
(i) (i) m(t)是在闭区间[t0, tf]上的分段连续函数（即只有有限个第一类间断点，在间断点处，假定是左连续的）；
(ii) (ii) m(t)在端点t0, tf处是连续的；
(iii)
(iii) 
这里U是R r中的有界闭集。
问题的提法 假设上面的(1),(2),(3),(4)式均已给定，要求从容许控制中求出一个控制
，它使系统(1)满足初始条件(2)的轨线，在终止时刻tf时达到目标集(3)，并使性能指标(4)取极小值（或极大值）。
为此引进协态变量（相对于状态变量
而言）。
它满足微分方程组
(5)
作辅助函数
(6)
称为系统(1)的哈密顿函数。这时可把方程组(1)和(5)表示为下面的形式：
(7)
称为哈密顿方程组或正则方程组。则有
最小值原理 如果
是上面所提问题的最优控制，
,
是正则方程组(7)对应于
的最优轨线和最优协态变量，则有
于是可按下列步骤求解：
(1) 写出哈密顿函数和正则方程组。
(2) 对
求哈密顿函数的最小值，找出关系式：
（8）
(3) 把关系式(8)代入正则方程组，根据下述边界条件，对正则方程组求解两点边值问题，即可求出最优轨线
和最优协态变量
：
(i) 假设方程组(1)已给初始条件
和终止条件(目标集)
，则正则方程组(7)的边界条件为：
, 
(ii) 假设
是给定的，没有给定目标集(3)，即
是自由的，则正则方程组(7)的边界条件为：
,
其中
是性能指标(4)中的第一项。若
，这时边界条件变为
,
(iii) 假设
是给定的，而终止状态满足目标集
并假定
是
维的，其中
，则正则方程组(7)的边界条件为
,
其中
是一个
维待定的常值列矢量。以上共有
个边界条件。
其次，假定
不固定，而是自由的。这时相当于边界条件中多了一个独立参数，因此要补充一个关系式。对于边界条件为(i)，(ii)的情形，补充的关系式为
对于边界条件为(iii)的情形，补充的关系式为
(4) 将求出的
,
代入关系式(8)，就可求得最优控制
。
以上步骤也可根据问题的性质，灵活应用。
对最大值原理有类似的说法。
说明 最小(大)值原理描述控制系统最佳性的必要条件，它给出一个确定最优控制
的方法。这一原理是由古典变分法引伸出来的。它可以推出变分法中熟知的一切必要条件，但是，它与古典变分法相比较，这一原理的主要优越性在于，它适用于任何集合
，特别它包含
是有界闭集的情形，而古典变方法只适用于
为开集或
的情形，因此这可以说是控制域类
的扩充。但它和变分法一样都遇到两点边值问题的困难。
[离散系统的最小(大)值原理] 考虑一离散型控制系统(图18。13)其状态方程为
(1)
并满足初始条件
(2)
终止状态
是自由的，性能指标为
(3)
式中
,
分别为系统对应于时刻
的状态矢量和控制矢量，他们分别是
维和
维矢量。
问题的提法 寻求
个控制矢量
满足初始条件(2)，使性能指标
取极小(大)值。
处理方法和连续情形相仿。引进
的协态变量
，它是
维列矢量。构造哈密顿函数
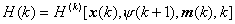
(4)
这时有正则方程组
,即
(5)
,即
(6)
离散型的最小值原理 设
为最优控制，
为相应的最优轨线，
为相应的最优协态变量，则它们满足正则方程(5)，(6)和下列条件下之一：
(i) 
,即
(ii) 
同时，满足边界条件(若
是预先给定的，则不要这条件)
(当
时，
)
于是可按下列步骤求解：
(1) (1) 写出哈密顿函数(4)和正则方程(5)，(6)。
(2)
(2) 固定
，
,对哈密顿函数
应用最小值原理的条件(i)或(ii)，求出关系式
(7)
(3) (3) 将关系式(7)代入正则方程组(5)，(6)中，并利用条件
,
把问题化为解方程组的两点边值问题。由此可以求出
和
。
(4)
(4) 将求出的
，
代入(7)，就得到最优控制
。
说明 离散系统的最小(大)值原理除某些特殊情形外不存在。参考G。S。G。Beveridge and R。S。Schechter, Opiimization: Theory and Practice。 1970, Mc Graw-Hill, Inc。, 第257－258页。