二、等距节点插值公式(差分公式)

[向前差分与向后差分]  已知函数f(x)在等距节点

                     

的值为

                          

其差分按下式计算

一阶差分                        

二阶差分      

…………………………

k阶差分  

                                           

符号称为向前差分。此外还可引进符号，它们的定义是

             

符号称为向后差分。

   向前差分和向后差分之间的关系为

                       

  [差分表]    

x	y
						B

  [牛顿第一插值公式(牛顿向前插值公式)]

  节    点            为步长）

  插 值 点                  （0<u<1）

  插值公式  

            

  余    项        

式中为二项系数。

  适用范围  通常用于计算插值区间的始点附近的函数值。

  [牛顿第二插值公式(牛顿向后插值公式)]

  节    点         (h>0)

  插 值 点   

  插值公式 

           

  余    项        

式中

            

用向后差分时

            

  适用范围  通常用于计算插值区间的终点附近的函数值。

  [斯特林插值公式]

节    点        

插 值 点 

插值公式 

          

余    项 

                           

适用范围  通常用于计算插值区间中点附近的函数值。一般当

时用这个公式。

注意事项  每次用的节点的个数都是奇数。

[贝塞尔插值公式]

节    点         

    插 值 点 

插值公式 

   

       

       

       

       

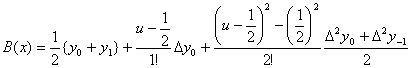
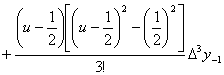
余   项       

    

                                   

     适用范围  通常用于计算两相邻节点之间的中点附近的函数值。这个公式一般在时使用。

     注意事项  每次用的节点的个数都是偶数。

     当时，插值公式特别简单:

      

     

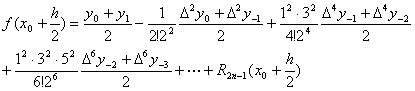
     说明  应用差分法插值时，并非项数愈多结果就愈精确，一般取二、三次就可以了。不难看出，线性插值法只是差分法的一个特例(取一阶差分)。