2、马尔科夫链

[马尔科夫链]  马尔科夫链是时间与状态都是离散的马尔科夫过程。

1^° 设在一系列随机试验下，系统的可能离散状态为E₀,E₁,L,如果对于任意二正整数k,m,任意整数0≤j₁<j₂<L<j_l<m,等式

都成立(表示“第m次试验出现E_m”的事件)，那末称这一随机试验列为马尔科夫链，简称马氏链。

2^°  随机变量序列{x_n}(n=0,1,L)为马尔科夫链的定义

设{x_n}(n=0,1,L)为一随机变量序列，它们中间的每一个都可能取值(相当于所处状态E_i) x_i(i=0,1,2,L),如果对于任意正整数k,m,任意正整数0≤j₁<j₂<L<j_l<m,等式

成立，就称{x_n}为马尔科夫链，简称马氏链。

通常可取{x_i}={1,2,L}。

马氏链所刻划的随机试验序列，可以直观地理解为要验测“将来”所处的状态只要用“现在”已知的状态，而“过去”的状态不起任何作用，这就是无后效性。

马氏链，以至于马尔科夫过程都是具有无后效性的随机过程。

[马尔科夫链的转移概率矩阵]  如果在时刻m系统由状态E_i经过一次转移到达状态E_j的概率和时刻m无关，那末就可用p_ij表示这个一次转移概率。显然

                        （p_ij≥0,i,j=0,1,2,L）

转移概率p_ij可排成一个转移概率矩阵

               

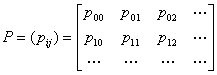
这是一个每行元素和为1的非负元素的矩阵，称为马氏链的一步转移概率矩阵。

同样用表示系统由状态E_i经过n次转移而到达状态E_j的转移概率，

同样定义马氏链的n步转移概率矩阵：

由无后效性，得

称为切普曼-柯尔莫哥洛夫方程。

由切普曼-柯尔莫哥洛夫方程可以推出

P⁽ⁿ⁾=Pⁿ

[闭集与状态的分类]  考虑时齐的马氏链。设E为状态空间，E=(E₀,E₁,E₂,L),如果存在正整数n使得，则称E_k可自E_j到达，并记为E_jÞE_k. 。如E_jÞE_k且E_kÞE_j，就说E_j，E_k,互通，记作E_jÛE_k。

称E的子集C为闭集，是指C外的任一状态都不能自C内任一状态到达。设E是闭集，若单点集{E_k}成一闭集，就称E_k为吸引状态，若E内不存在真子集是闭集，称这个马氏链是不可分的。

记“系统处在状态E_i的条件下，经n步转移初次到状态E_j”的条件概率为，它可用转移概率表示为

                    

于是

记

它是“系统在开始处于状态E_i的条件下，经有穷次转移后终于到达状态E_j”的条件概率，并令

如f_ij=1,则可视m_ij为从状态E_i出发，初次到达状态E_j转移次数的数学期望

状态分类如下：

1° 如果f_jj=1,则称E_j为常返的；如果f_jj<1，则称E_j为非常返的；

2° 设E_j是常返状态，若m_jj=∞，则称E_j为消极常返的(或零状态)；若μ_jj<∞,则称E_j为积极常返的(或正状态)。

3° 如果正整数集有最大公约数t，当t>1,称E_j为周期的，或具有周期t;当t=1,则称E_j为非周期的。

4° 如果E_j是常返，非周期正状态，则称E_j为遍历的。

状态分类的判别法

1°  E_j为非常返的充分必要条件是。

2°  若E_j是有周期t的常返状态，则。

3°  若E_j是遍历的，则。

4°  若E_j是常返的，则它为零状态的充分必要条件是。

[马尔科夫链的分解定理]  任一系统的状态空间可以分解为下列不交子集D,C₁,C₂,L之和，其中

1^°  任一C_j是由常返状态构成的不可分的闭集，C_i中的状态不能自C_j(i≠j)中的状态到达；

2^°  C_j中的状态属同类：或者都是零的，或者都是遍历的，或者都是有周期的非零的状态(在任何一种情况下，C_j中各状态都有相同的周期)，而且f_ik=1(E_iÎC_j,E_kÎC_j);

3^°  D由一切非常返状态构成(C_j中的状态可能自D中的状态到达，反过来不行)。

[马尔科夫链的遍历性定理]  对于不同的类型，有如下的遍历性定理：

1^°  若E_kÎD或E_k为零状态，则对任意的j，有

2^°  若E_k是周期为t的正的常返状态，则对任意的j，有

  (1≤r≤t)

其中                         

表示自E_j出发，在某n步(n≡r(modt))上初次到达E_k的概率。

3^°  对于不可分非周期的马氏链，极限

存在，而且只能有下面两种情况：

（i）所有p_j(出现E_j的概率)都大于零，此时{p_j}是唯一的平稳分布，即概率分布{p_j}满足

    （j=0,1,L）

（ii）所有的p_j都等于零，此时不存在平稳分布。