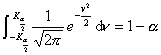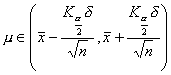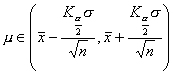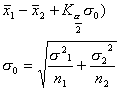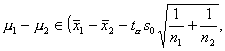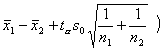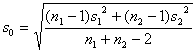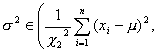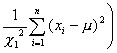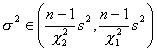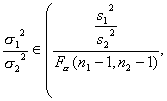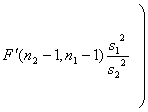5、总体参数的区间估计
[小概率原理] 在一次试验中,概率很小(接近于零)的事件认为是实际上不可能发生的事件;而概率接近于1的事件认为是实际上必然发生的事件。
[置信区间与显著性水平] 对总体参数![]() (如
(如![]() )进行区间估计(即估计参数的取值范围)时,如果对于预先给定的很小的概率
)进行区间估计(即估计参数的取值范围)时,如果对于预先给定的很小的概率![]() ,能找到一个区间(
,能找到一个区间(![]() ),使得
),使得
![]() =1-
=1-![]()
那末称区间(![]() )为参数
)为参数![]() 的置信区间,
的置信区间,![]() 和
和![]() 称为置信限(或临界值);
称为置信限(或临界值);![]() 和
和![]() 称为否定域;概率
称为否定域;概率![]() 称为显著性水平,1-
称为显著性水平,1-![]() 称为置信水平(或置信概率)。
称为置信水平(或置信概率)。
[总体参数的区间估计表] 假设总体遵从正态分布![]()
![]() )。对于预先给的显著性水平
)。对于预先给的显著性水平![]() ,可用一个样本x1, x2 ,···,xn的均值
,可用一个样本x1, x2 ,···,xn的均值![]() 和标准差s来估计总体的均值
和标准差s来估计总体的均值![]() 和方差
和方差![]() 的置信区间,也可用两个样本
的置信区间,也可用两个样本![]() 与
与![]() 的均值
的均值![]() 和标准差
和标准差![]() 来估计两总体均值差
来估计两总体均值差![]() 的置信区间。
的置信区间。
|
样本情况 |
总体参数 |
与置信区间有关的 |
|
大样本 已知总体方差
|
|
查正态分布表 |
|
大样本 总体方差未知 |
|
同上 |
|
小样本 已知总体方差
|
|
同上 |
|
小样本 总体方差未知 |
|
查t分布表(自由度为n-1) |
|
已知两总体的 方差 |
|
查正态分布表 |
|
两总体的方差 未 知 |
式中 |
查t分布表 (自由度为n1 + n2-2 ) |
|
小样本 已知总体均值 |
|
查 (自由度为n) |
|
小样本 总体均值未知 |
|
查 (自由度为n |
|
小样本 两总体的均值 与方差未知 |
|
查F分布表 (自由度为
查 (自由度为(n2 -1,n1 –1)) |