3、总体参数的点估计
记x1 ,x2 ,···,xn是从总体![]() 中取出的一个样本,可用样本的特征数来估计总体的数字特征。其常用方法有以下两种:
中取出的一个样本,可用样本的特征数来估计总体的数字特征。其常用方法有以下两种:
[矩法] 矩法是用样本的r阶矩作为总体r阶矩的估值。具体步骤如下:
设![]() 的分布函数包含k个参数
的分布函数包含k个参数![]() (其取值未知),记作
(其取值未知),记作![]() 。假定
。假定![]() 的k阶原点矩存在,它们自然是
的k阶原点矩存在,它们自然是![]() 的函数,即
的函数,即
![]() (r=1,2,···,k)
(r=1,2,···,k)
考虑总体的一个样本![]() 作出这一样本的r阶矩
作出这一样本的r阶矩![]() ,即
,即
![]() =
=![]()
然后解方程组
![]() (
(![]() =
=![]() (r=1,2,···,k)
(r=1,2,···,k)
记所得的解为
![]()
用![]() 分别作为
分别作为![]() 的估值。
的估值。
[最大似然法] 设总体的分布是连续型的,分布密度函数为![]() ,其中
,其中![]() 是待估计的未知参数。对于给定的
是待估计的未知参数。对于给定的![]() 使函数
使函数![]() 达到最大值的
达到最大值的![]() ,并用它们分别作为
,并用它们分别作为![]() 的估值。
的估值。
由于ln![]() 与
与![]() 在同一点(
在同一点(![]() )上达到最大值,因此,引入函数
)上达到最大值,因此,引入函数
L(![]() )=ln
)=ln![]() =
=![]()
![]() )
)
它称为似然函数。只要解方程组
![]() (i=1,2,···,k)
(i=1,2,···,k)
就可以从中确定所要求的![]() ,它们分别称为参数
,它们分别称为参数![]() 的最大似然估计值。
的最大似然估计值。
如果总体的分布是离散型的,只要把上述似然函数中的![]() 取为
取为![]() 就可以了。
就可以了。
例 正态总体的参数估计,假定已知总体遵从正态分布N(![]() ,但参数
,但参数![]() 未知。现在要用总体的n次观测值x1
, x2 ,···, xn求
未知。现在要用总体的n次观测值x1
, x2 ,···, xn求![]() 的最大似然估值。
的最大似然估值。
解 因为总体的分布密度函数为
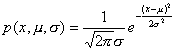
因此,似然函数为
![]()
解方程组

得
![]()
![]()
容易检验![]() 确实使
确实使![]() 取到最大值。因此它们分别是
取到最大值。因此它们分别是![]() 的最大似然估值。
的最大似然估值。
[估值好坏的判别标准]
1° 无偏性 如果参数![]() 的估值
的估值![]() x1
, x2 ,···, xn)满足关系式
x1
, x2 ,···, xn)满足关系式
![]()
则称![]() 是
是![]() 的无偏估值。
的无偏估值。
2° 有效性 如果![]() 和
和![]() 都是参数
都是参数![]() 的无偏估值。
的无偏估值。
![]()
则称![]() 比
比![]() 有效。进一步,如果固定样本的容量n,使
有效。进一步,如果固定样本的容量n,使![]() 极小值的无偏估值
极小值的无偏估值![]() 就称为
就称为![]() 的有效估值。
的有效估值。
3° 一致性 如果对任意给定的正数![]() ,总有
,总有
![]()
则称![]() 的估值
的估值![]() 是一致的。
是一致的。
由契贝谢夫不等式(见§1,三)易见,当
![]()
对某![]() 成立时,
成立时,![]() 是
是![]() 的一致估值。
的一致估值。
在实用中,往往应用这一充分条件来验证![]() 是否是
是否是![]() 的一致估值。
的一致估值。
例
|
总体分布 |
未知总体 参 数 |
总体参数估值 |
无偏性 |
有效性 |
一致性 |
|
|
|
|
有 有 有 有 有 有 有 |
有 有 有 有 |
有 有 有 有 有 有 |