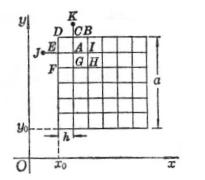
2. 椭圆型方程的差分方法
[五点格式] 考虑拉普拉斯方程的第一边值问题
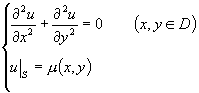
式中![]() 为定义在D的边界S上的已知函数.
为定义在D的边界S上的已知函数.
采用正方形网格,记![]() ,在节点(i, j)上分别用差商
,在节点(i, j)上分别用差商
![]()
代替![]() ,对应的差分方程为
,对应的差分方程为
![]() (1)
(1)
或
![]()
即任一节点(i,
j)上![]() 的值等于周围相邻节点上解的值的算术平均,这种形式的差分方程称为五点格式,在边界节点上取
的值等于周围相邻节点上解的值的算术平均,这种形式的差分方程称为五点格式,在边界节点上取
![]() (2)
(2)
式中![]() 是与节点(i, j)最接近的S上的点.于是得到了以所有内节点上的
是与节点(i, j)最接近的S上的点.于是得到了以所有内节点上的![]() 值为未知量的若干个线性代数方程,由于每一个节点都可列出一个方程,所以未知量的个数与方程的个数都等于节点的总数,于是,可用通常的方法(如高斯消去法)解此线性代数方程组,但当步长不很大时,用高斯消去法将会遇到很大困难,可用下面介绍的其他方法求解.
值为未知量的若干个线性代数方程,由于每一个节点都可列出一个方程,所以未知量的个数与方程的个数都等于节点的总数,于是,可用通常的方法(如高斯消去法)解此线性代数方程组,但当步长不很大时,用高斯消去法将会遇到很大困难,可用下面介绍的其他方法求解.
若h0时,差分方程的解收敛于微分方程的解,则称差分方程为收敛的.
在计算过程中,由于进行四则运算引起舍入误差,每一步计算的舍入误差都会影响以后的计算结果,如果这种影响所产生的计算偏差可以控制,而不至于随着计算次数的增加而无限增大,则称差分方程是稳定的.
[迭代法解差分方程] 在五点格式的差分方程中,任意取一组初值{![]() },只要求它们在边界节点(i, j)上取以已知值
},只要求它们在边界节点(i, j)上取以已知值![]() ,然后用逐次逼近法(也称迭代法)解五点格式:
,然后用逐次逼近法(也称迭代法)解五点格式:
![]()
逐次求出{![]() }.当(i+1, j),(i-1, j),(i, j-1),(i, j+1)中有一点是边界节点时,每次迭代时,都要在这一点上取最接近的边界点的值.当n→∞时,
}.当(i+1, j),(i-1, j),(i, j-1),(i, j+1)中有一点是边界节点时,每次迭代时,都要在这一点上取最接近的边界点的值.当n→∞时,![]() 收敛于差分方程的解,因此n充分大时,{
收敛于差分方程的解,因此n充分大时,{![]() }可作差分方程的近似解,迭代次数越多,近似解越接近差分方程的解.
}可作差分方程的近似解,迭代次数越多,近似解越接近差分方程的解.
[用调节余数法求节点上解的近似值] 以差商代替Δu时,用节点(i+1, j),(i-1, j),(i, j+1),(i, j-1)上u的近似值来表示u在节点(i, j)的值将产生的误差,称此误差为余数![]() ,即
,即
![]()
|
图14.8 |
设在(i, j)上给![]() 以改变量
以改变量![]() ,从上式可见
,从上式可见![]() 将减少4
将减少4![]() ,而其余含有
,而其余含有![]() 的差分方程中的余数将增加
的差分方程中的余数将增加![]() ,多次调整
,多次调整![]() 的值就可将余数调整到许可的有效数字的范围内,这样可获得各节点上u(x, y)的近似值.这种方法比较简单,特别在对称区域中计算更简捷.
的值就可将余数调整到许可的有效数字的范围内,这样可获得各节点上u(x, y)的近似值.这种方法比较简单,特别在对称区域中计算更简捷.
例 求Δu=0在内节点A,B,C,D上解的近似值.设在边界节点1,2,3,4上分别取值为1,2,3,4(图14.8)
解 记u(A)=![]() ,点A,B,C,D的余数分别为
,点A,B,C,D的余数分别为
-4![]() + uB+ uc
+5=
+ uB+ uc
+5=![]()
![]() -4 uB +
uD+7=RB
-4 uB +
uD+7=RB
![]() -4 uc+ uD+3=RC
-4 uc+ uD+3=RC
uB+ uc-4uD+5=RD
以边界节点的边值的算术平均值作为初次近似值,即
![]() =uB(0)=uC(0)=uD(0)=2.5
=uB(0)=uC(0)=uD(0)=2.5
则相应的余数为:
![]() =0, RB=2, RC= -2, RD=0
=0, RB=2, RC= -2, RD=0
最大余数为±2.先用δuC=-0.5把RC缩减为零,uC相应地变为2,这时![]() ,
RD也同时缩减(-0.5),新余数是
,
RD也同时缩减(-0.5),新余数是![]() =-0.5,RB=2,
=-0.5,RB=2,![]() , RD=-0.5.类似地再变更δuB=0.5,从而 uB变为3,则得新余数为
, RD=-0.5.类似地再变更δuB=0.5,从而 uB变为3,则得新余数为![]() .这样便可消去各节点的余数,于是u在各节点的近似值为:
.这样便可消去各节点的余数,于是u在各节点的近似值为:
![]() =2.5, uB=3, uC=2,
uD=2.5
=2.5, uB=3, uC=2,
uD=2.5
现将各次近似值及余数列表如下:
|
次数 |
调 整 值 |
第n次近似值及余数 |
|||||||
|
|
|
uB |
RB |
uC |
RC |
uD |
RD |
||
|
0 1 2 |
δuC = -0.5 δuB = 0.5 |
2.5 2.5 2.5 |
0 -0.5 0 |
2.5 2.5 3 |
2 2 0 |
2.5 2 2 |
-2 0 0 |
2.5 2.5 2.5 |
0 -0.5 0 |
|
结果近似值 |
2.5 |
|
3 |
|
2 |
|
2.5 |
|
|
[解重调和方程的差分方法] 在矩形D(x0≤x≤x0+a,y0≤y≤y0+a)中考虑重调和方程
![]()
取步长![]() ,引直线族
,引直线族
 (i,
j = 0, 1, 2
(i,
j = 0, 1, 2![]() n)
n)
作成一个正方形网格.用差商代替偏导数
|
上式表明了以(x, y)为中心时,u(x, y)的函数值与周围各点函数值的关系,但对于邻近边界节点的点(x, y),如图14.9中的A,就不能直接使用上式,此时将划分网格的直线族延伸,在延伸线上定出与边界距离为h的点,称这些点为外邻边界节点,如图14.9以A为中心时,点E,C为边界节点,点J,K为E,C的外邻边界节点,用下法补充定义外邻边界节点J处函数的近似值uJ,便可应用上面的公式. 1° 边界条件为
图14.9 |
![]()
时,定义![]() .
.
2° 边界条件为
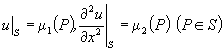
时,定义![]() .
.
[其他与Δu有关的网格]
1° 三角网格(图14.10(a))
取P0(x, y)为中心,它的周围6个邻近节点分别为:
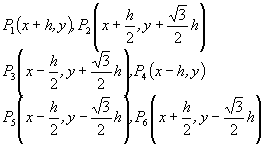
则
![]()
式中![]() ,R表示余项.
,R表示余项.
2° 六角网格(图14.10(b))
取P0(x, y)为中心,它的三个邻近节点分别为
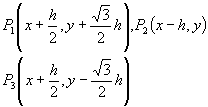
则
![]() .
.
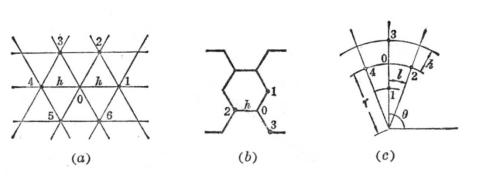
图14.10
3° 极坐标系中的网格(图14.10(c))
取P0(r,![]() )为中心,它的四个邻近节点分别为
)为中心,它的四个邻近节点分别为
![]()
而拉普拉斯方程
![]()
的相应的差分方程为
![]()