四、一阶非线性方程

    [完全解·通解·奇异解]  一阶非线性方程的一般形式为

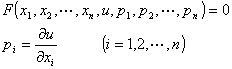
    若一阶偏微分方程的解包含任意n个独立的常数，则称这样的解为完全解(全积分).

    若V ( x₁, x₂  x_n , u , c₁ , c₂c_n ) = 0为方程的完全解，从

消去c_i ，若得一个解，则称它为方程的奇异解(奇积分).

    以两个独立变量为例说明完全解与通解、奇异解的关系，设方程

有完全解

V (x,y,z,a,b)=0          ( a,b为任意常数),

则方程等价于从方程组

消去a,b所得的方程.

    利用常数变易法把a,b看作x, y的函数，将V (x,y,z,a,b)=0求关于x, y的偏导数，得

那末

与V=0联立可确定a,b.有三种情况：

    1°  ，将其与V(x,y,z,a,b)=0联立可确定不含任意常数的奇异解.

    2°  如，即回到完全解.

    3°  当时，必有，这时，如果不属于情形2° ，则a与b存在函数关系：b=(a)，这里为任意可微函数，并从方程V(x,y,z,a,b)=0和消去a,b，可确定方程的通解.

    定理  偏微分方程的任何解包含在完全解内或通解内或奇异解内.

    [特征方程·特征带·特征曲线·初积分]  在一阶非线性方程：

中，设F对所有变量的二阶偏导数存在且连续，称

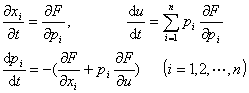
或

为非线性方程的特征方程.设特征方程的解为x_i=x_i(t),u=u(t),p_i=p_i(t)   (i=1,2,…,n)称它为非线性方程的特征带.在x₁,x₂x_n,u空间的曲线x_i=x_i(t), u=u(t)(i=1,2,…,n)称为非线性方程的特征曲线.如果函数在特征方程的任一解x_i=x_i(t) (i=1,2n), u=u(t), p_i=p_i(t)   (i=1,2n)上等于常数，即

那末函数称为特征方程的初积分.

    [求完全解的拉格朗日－恰比方法]  考虑两个变量的情况.

    对于方程F(x,y,z,p,q)=0，选择使雅可比式的一个初积分G(x,y,z,p,q).解方程组

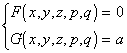     (a为任意常数)

得p(x,y,z,a)及q(x,y,z,a).则方程

dz=pdx+qdy

的通解V(x,y,z,a,b)=0(b是积分dz=pdx+qdy出现的任意常数)就是方程F(x,y,z,p,q)=0的完全解.

    例  求方程的完全解.

    解  方程的特征方程为

这里成立

所以特征方程的一个初积分为z²p² －x² .

    解方程组                  (a为任意常数)

得                            

积分微分方程

得完全解

   (b为任意常数)

    [某些容易求完全解的方程]

    1°  仅含p,q的方程F(p,q)=0

    G=p是特征方程的一个初积分.从F(p,q)=0与p=a(a为任意常数)得q=(a)，积分

dz=adx+(a)dy

得完全解

z=ax+(a)y+b    (b为任意常数)

    2°  不显含x,y的方程F(z,p,q)=0

    特征方程为

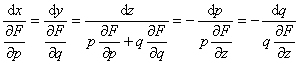
因此qdp-pdq=0，显然为一个初积分，由F(z,p,q)=0，q=pa(a为任意常数)解得p=(z,a).于是由

dz=(z,a)dx+a(z,a)dy

得

      (b为任意常数)

可确定完全解.

    3°  变量分离形式的方程

特征方程为

可取初积分G_i=f_i(x_i,p_i) ,  (i=1,2n).从f_i(x_i,p_i)=a_i    (i=1,2n)解出

p_i=_i(x_i,a_i)

得完全解

式中a_i,b为任意常数，且.

    [克莱罗方程]  方程

称为克莱罗方程，其完全解为

对c_i微分得

       (i=1,2,…,n)

与完全解的表达式联立消去c_i即得奇异解.

    例  求方程z－xp－yq－pq=0的完全解和奇异解.

    解  这是克莱罗方程，它的完全解是

z=ax+by+ab

    对a,b微分，得x=－b,y=－a，消去a,b得奇异解

z=－xy

    [发甫方程]  方程

P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz=0                                   (1)

称为发甫方程，如果P,Q,R二次连续可微并满足适当条件，那末方程可积分.如果可积分成一关系式时，则称它为完全可积.

    1°  方程完全可积的充分必要条件   当且仅当P,Q,R满足条件

                                   (2)

时，存在一个积分因子(x,y,z)，使

dU₁=(Pdx+Qdy+Rdz)

从而方程的通解为

U₁(x,y,z)=c

    特别，当时，存在一个函数U(x,y,z)满足

从而                             dU=Pdx+Qdy+Rdz

    所以方程的通解为

U(x,y,z)=c

    所以完全可积的发甫方程的通解是一单参数的曲面族.

    定理  设对于发甫方程(1)在某区域D上的完全可积条件(2)成立，则对D内任一点M(x,y,z)一定有方程的积分曲面通过，而且只有一个这样的积分曲面通过.

    2°  方程积分曲面的求法

    设完全可积条件(2)成立.为了构造积分曲面，把z看成x,y的函数(设R(x,y,z)≠0)，于是原方程化为

由此得方程组

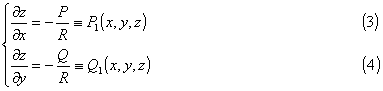
发甫方程(1)与此方程组等价.

    把方程(3)中的y看成参变量，积分后得一个含有常数的通解

然后用未知函数代替常数，将代入方程(4)，在完全可积的条件下，可得的一个常微分方程，其通解为

c为任意常数，代回中即得发甫方程的积分曲面

z=(x,y,(y,c))

    由于发甫方程关于x,y,z的对称性，在上面的讨论中，也可把x或y看成未知函数，得到同样的结果.

    例  求方程yzdx+2xzdy+xydz=0的积分曲面族.

    解  容易验证完全可积条件成立，显然存在一个积分因子，用它乘原方程得

积分后得积分曲面族

xy²z=c

    也可把方程化为等价的方程组

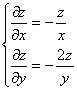
把y看成参变量，积分得通解

用未知函数代替，将代入方程得

积分后有

所以原方程的积分曲面族是

xy²z=c