二、一阶线性方程

    1．    一阶齐次线性方程

    [特征方程 特征曲线 初积分(首次积分)]  给定一阶齐次线性方程

                     (1)

 

式中ai为连续可微函数，在所考虑的区域内的每一点不同时为零(下同).方程组

      ( i = 1,2n )          

或

                (2)

称为一阶齐次线性偏微分方程的特征方程.如果曲线l: xi = xi (t) ( i=1,2n )满足特征方程(2)，就称曲线l为一阶齐次线性方程的特征曲线.

    如果函数 ( x1 , x2 xn )在特征曲线上等于常数，即

( x1(t) , x2(t)  xn(t) ) = c

就称函数 ( x1, x2 xn )为特征方程(2)的初积分(首次积分).

    [齐次方程的通解]

    1o  连续可微函数u = ( x1, x2 xn ) 是齐次线性方程(1)的解的充分必要条件是： ( x1, x2 xn )是这个方程的特征方程的初积分.

    2o  设i ( x1 , x2  xn )  ( i = 1,2 n) 是特征方程(2)在区域D上连续可微而且相互独立的初积分(因此在D内的每一点，矩阵

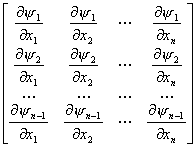
的秩为n) ，则

u = ( 1 ( x1 , x2  xn )  n-1 ( x1 , x2  xn ) )

是一阶齐次线性方程(1)的通解，其中为n个变量的任意连续可微函数.

    [柯西问题]  考虑方程的柯西问题

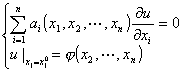
式中 ( x2  xn )为已知的连续可微函数.

    设i ( x1 , x2  xn )  ( i = 1,2 n) 为特征方程的任意n个相互独立的初积分，引入参变量  ()，从方程组

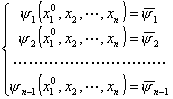
解出x2  xn 得

则柯西问题的解为

u = ( 2 ( 1 , 2  n-1 )  n ( 1 , 2  n-1 ) )