§2 一阶偏微分方程

一、        柯西-柯娃列夫斯卡娅定理

    [一阶偏微分方程的通解]  一阶偏微分方程的一般形式*是

或

，其中

如解出p₁，可得：

p₁ = f (x₁ , x₂ ,…, x_n , u , p₂ ,…, p_n )

    当方程的解包含某些“任意元素”(指函数)，如果适当选取“任意元素”时，可得方程的任意解(某些“奇异解”除外)，则称这样的解为通解.

    在偏微分方程的研究中，重点在于确定方程在一些附加条件(即定解条件)下的解，而不在于求通解.

    [一阶方程的柯西问题]

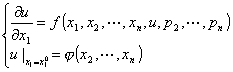
称为柯西问题，式中为已知函数，对柯西问题有如下的存在惟一性定理.

    [柯西－柯娃列夫斯卡娅定理]    设 f ( x₁ , x₂ x_n , u , p₂  p_n ) 在点 ( x₁⁰ , x₂⁰  x_n⁰ , u⁰ , p₂⁰  p_n⁰ ) 的某一邻域内解析，而在点( x₂⁰ x_n⁰ ) 的某邻域内解析，则柯西问题在点 ( x₁⁰  x_n⁰ ) 的某一邻域内存在着惟一的解析解.

    这个定理应用的局限性较大，因它要求f及初始条件都是解析函数，一般的定解问题未必能满足这种条件.

    对高阶方程也有类似定理.