2.  常系数线性微分方程组

    微分方程组

                                       (3)

称为常系数线性微分方程组，式中a_ij是常数.当f_i(t)≡0 (i=1,2,…,n)，称(3)为齐次的，当f_i(t)不全恒等于零，称(3)为非齐次的.

    [特征根与齐次方程组的线性无关解]

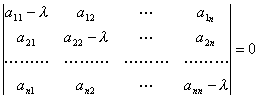
是λ的n次代数方程，它称为非齐次线性微分方程组(3)所对应的齐次线性微分方程组的特征方程，特征方程的根称为特征根.

根据特征根的不同情形，给出齐次线性微分方程组线性无关解的不同形式.

特征根λ	线性无关解中相应的解的形式	说   明
λ是单实根	( j = 1, 2,…,n )	Aj是待定常数
λ是r重实根	( j = 1, 2,…,n )	Pj(t)是系数待定的次数不超过r-1次的多项式
λ=α±iβ是k重复根	( j = 1, 2,…,n )	Qj(t) ，Rj(t)是系数待定的次数不超过k-1次的多项式

    [用常数变易法求非齐次方程组的特解]  非齐次线性微分方程组(3)的一个特解，可由对应的齐次线性微分方程组的通解利用常数变易法求得.

    设y₁₁,y_21,…,y_n1;y₁₂,y₂₂,…,y_n2;…;y_1n,y_2n,…,y_nn是对应的齐次线性微分方程组的n个线性无关解.那末非齐次线性方程组的一个特解y₁*,y₂*,…,y_n*可由下列形式确定

式中c_i(t)是待定函数，它们满足下列方程组：

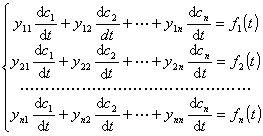
从上面方程组解出，再积分就得出所要求的c_i(t) (i=1,2,…,n)

    例  求解微分方程组：

                                               (1)

    解  先求对应的齐次线性微分方程组

                                                 (2)

的通解.由特征方程

可知特征根为λ=5,.则相应的线性无关解是如下形式：

                          

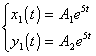
分别代入齐次线性方程组(2)，利用待定系数法，确定出

A₁=c₁ , A₂=2_c1 ,      （c₁ 是任意常数）

B₁=c₂ , B₂= ,      （c₂ 是任意常数）

所以齐次线性方程组 (2)的通解为

          （c₁ ,c₂ 是任意常数）

    其次，利用常数变易法求非齐次线性方程组(1)的一个特解.把c₁ ,c₂看成是t的函数，解下列方程组

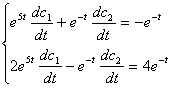
得

积分后，取

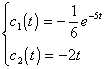
于是所求方程组(1)的通解是

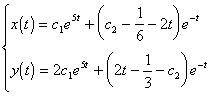
式中c₁ ,c₂为任意常数.