四、傅立叶级数的收敛性及在第一类间断点的性质

[傅立叶级数收敛性的判别]

1^o  假设的傅立叶级数的部分和为

如果当,s_m(x)趋于(在某一点x趋于，或在某一区间内一致地趋于)函数，那末函数的傅立叶级数收敛于函数.

2^o  如果函数在开区间内分段单调，并在该区间内有有限个第一类间断点，那末(i) s_m(x)在连续点x收敛于
；(ii)在第一类间断点x₀收敛于；(iii)在区间的端点，即 与上，等于
.(狄利克莱定理)

3^o  如果函数在区间上分段可微，在连续点上有导数，在第一类间断点x₀处极限

和

存在，那末s_m(x)在连续点x上收敛于，在间断点x₀上收敛于

[吉布斯现象]  以为周期的函数具有第一类间断点，令，在点函数的跳跃为
，假定函数在点的某邻域内没有其他间断点，且有有界变差.令函数
的傅立叶级数部分和为s_m(x).那末函数的傅立叶级数在点处是收敛的，但在该邻域内不一致收敛.这时
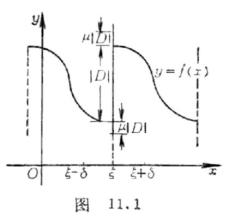
有一种奇怪的现象(称为吉布斯现象)出现：

存在点列，和，使得

                   

                   

               

因此，s_m(x)在间断点的邻域内的振幅的极限为  

         

它比函数在点的跳跃量大(约18%)，或者是的
倍(图11.1).

    例  函数

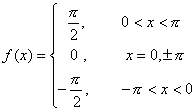
的傅立叶级数为

～

点x=0为的第一类间断点,其跳跃D=π

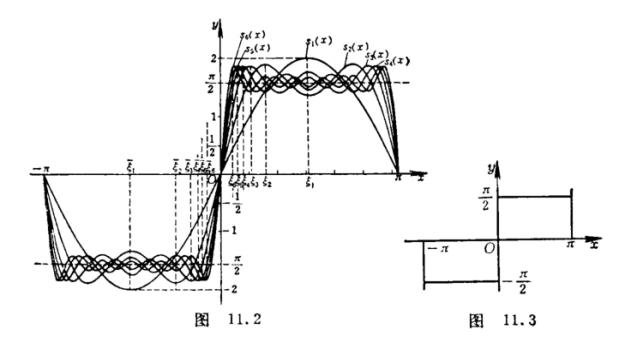
y =s_m(x) (m=1,2,3,4,5,6)的曲线如图11.2.

存在点列 ,  ,使得

当时，s_m(x)的极限图形如图11.3(注意在点x=0的形状).