二、留数定理及其应用
[留数的定义] 设点![]() 是函数
是函数![]() 的孤立奇点,
的孤立奇点,![]() 是圆周
是圆周![]() ,称积分
,称积分
![]()
的数值为函数![]() 在孤立奇点
在孤立奇点![]() 处的留数(残数),记作
处的留数(残数),记作![]() ,这里
,这里![]() 为适当小的正数(使圆内无
为适当小的正数(使圆内无![]() 的其它奇点),留数值与
的其它奇点),留数值与![]() 的取值无关.
的取值无关.
函数![]() 在一个孤立奇点
在一个孤立奇点![]() 处的留数等于
处的留数等于![]() 在点
在点![]() 的邻域内的罗朗展开式中负一次幂的系数,即
的邻域内的罗朗展开式中负一次幂的系数,即
![]()
[孤立奇点的留数计算法则]
1o 函数在可去奇点的留数等于零.
2o 设![]() 是
是![]() 的一阶极点,则
的一阶极点,则
![]()
3o 设![]() 是
是![]() 的
的![]() 阶极点,则
阶极点,则
![]()
4o 设分式函数![]() ,
,![]() 和
和![]() 在点
在点![]() 解析,
解析,![]() 是
是![]() 的一阶零点,而
的一阶零点,而![]() ,则
,则
![]() (
(![]() 为
为![]() 在
在![]() 的导数)
的导数)
5o 设![]() 是
是![]() 的孤立奇点,
的孤立奇点,![]() 表示半径足够大的圆周
表示半径足够大的圆周![]() (使圆周外部无
(使圆周外部无![]() 的其他奇点),称积分
的其他奇点),称积分
![]()
的数值为![]() 在
在![]() 的留数(其中
的留数(其中![]() 是取顺时针方向),记作
是取顺时针方向),记作![]() ,所以
,所以
![]()
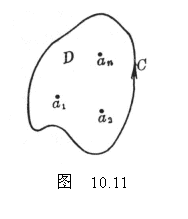
[留数定理] 如果函数![]() 在简单闭曲线
在简单闭曲线![]() 的内部
的内部![]() 内除了有限个奇点
内除了有限个奇点![]() 外解析,并且在
外解析,并且在![]() 上除了
上除了![]() 外连续,那末
外连续,那末
![]()
[辐角原理] 如果函数![]() 在简单闭曲线
在简单闭曲线![]() 的内部
的内部![]() 内除了有限个阶数分别是
内除了有限个阶数分别是![]() 的极点
的极点![]() 外解析,在
外解析,在![]() 上除了点
上除了点![]() 外连续,在
外连续,在![]() 上没有零点与极点,而在
上没有零点与极点,而在![]() 内有阶数分别是
内有阶数分别是![]() 的零点
的零点![]() ,那末
,那末
![]()
其中![]() 表示点
表示点![]() 沿曲线
沿曲线![]() 移动一圈后
移动一圈后![]() 的辐角改变量.设
的辐角改变量.设![]() 是曲线
是曲线![]() 在映射
在映射![]() 下的象,则
下的象,则![]() 称为曲线
称为曲线![]() 的回转次数.
的回转次数.
[儒歇定理] 如果函数![]() 与
与![]() 在简单闭曲线
在简单闭曲线![]() 及
及![]() 的内部
的内部![]() 解析,且在
解析,且在![]() 上
上
![]() ,
, ![]()
那末在![]() 的内部,
的内部,![]() 和
和![]() 有相同的零点个数,即
有相同的零点个数,即
![]()
[利用留数定理计算定积分]
1o 计算积分![]()
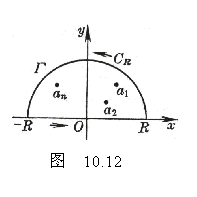 如果
如果![]() 除在实轴的上侧有有限多个孤立奇点
除在实轴的上侧有有限多个孤立奇点![]() 外,在包括实轴在内的上半平面上处处是解析的,同时假设
外,在包括实轴在内的上半平面上处处是解析的,同时假设![]() 是
是![]() 的至少二阶的零点,或者
的至少二阶的零点,或者
![]() (
(![]() ,
,![]() 为常数)
为常数)
那末可按照下列步骤计算积分![]() (图10.12):
(图10.12):
(1)
(1)作辅助函数![]() ,在实轴上
,在实轴上
![]()
(2)
(2)作附加积分路线![]() ,使它和
,使它和![]() 合起来变成一条包含
合起来变成一条包含![]() 的所有奇点
的所有奇点![]() 的闭曲线
的闭曲线![]() ,则
,则
![]()
(3)
(3)求出![]() 在上半平面的各奇点的留数总和,应用留数定理,有
在上半平面的各奇点的留数总和,应用留数定理,有
![]()
(4)
(4)令![]() ,根据假设,
,根据假设,![]() ,那末
,那末
例1
例1
计算![]()
解 ![]()
(1) (1) 作辅助函数![]() .
.
(2) (2) 作附加积分线路![]() :以原点为中心,半径
:以原点为中心,半径![]() 充分大的上半圆周(图10.13).
充分大的上半圆周(图10.13).
(3) (3) ![]() 在上半平面只有一个极点
在上半平面只有一个极点![]() ,其留数为
,其留数为

![]()
(4)
![]()
所以
![]()
2o 计算积分 ![]() (
(![]() )
)
设![]() 是有理函数,并且分母的次数
是有理函数,并且分母的次数![]() 分子的次数
分子的次数![]() (
(![]() ).
).
计算的基本步骤和上面一样,它的辅助函数是![]() ,附加积分路线和积分闭曲线
,附加积分路线和积分闭曲线![]() 分下面两种情况:
分下面两种情况:
(a)
(a)如果![]() 在实轴上有有限多个一阶极点,积分闭曲线
在实轴上有有限多个一阶极点,积分闭曲线![]() (在极点处,以各极点为圆心,
(在极点处,以各极点为圆心,![]() 为半径在下半平面作半圆,为正向)见图10.14(a)*,那末
为半径在下半平面作半圆,为正向)见图10.14(a)*,那末
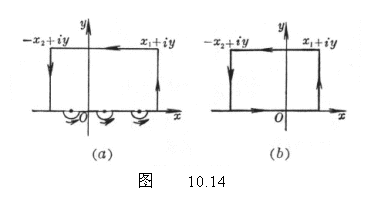
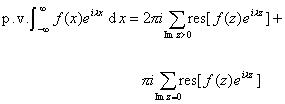
这里的广义积分是柯西主值,其定义见第六章§1,五.
(b)
(b)如果![]() 在实轴上没有奇
在实轴上没有奇
点,积分闭曲线见图10.14(b).
![]()
例2
例2 计算积分![]() (
(![]() )
)
解 作辅助函数![]() ,它只有实轴上的两个奇点
,它只有实轴上的两个奇点![]() ,
,![]() ,所以由(a)
,所以由(a)
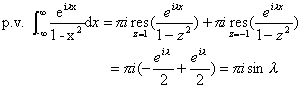
例3
例3 计算积分![]()
解 (1)作辅助函数![]() .
.
(2)作附加积分线路![]() 和
和![]() 与
与![]() ,
,![]() 合起来变成一条包含奇点
合起来变成一条包含奇点![]() 的闭曲线
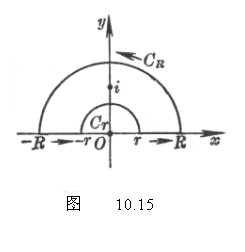
的闭曲线![]() (图10.15),则
(图10.15),则
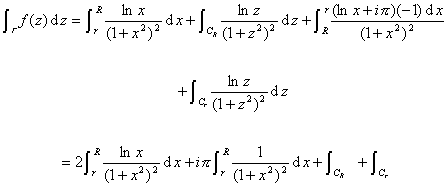
(3)在![]() 曲线内函数
曲线内函数![]() 只有一个二阶极点
只有一个二阶极点![]() ,根据孤立奇点的留数计算法则3o,得到
,根据孤立奇点的留数计算法则3o,得到![]() 处
处![]() 的留数,则
的留数,则
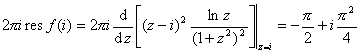
(4)可以证明当![]() ,
,![]() 时,积分
时,积分![]() ,
,![]() ,于是得
,于是得
![]()
上式两边实部相等,所以
![]()