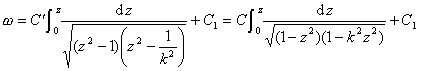四、对称原理与多边形映射

    [对称原理]  设和是平面上关于它们公共边界（一段圆弧）对称的两个区域，而和是平面上关于它们公共边界（一段圆弧）对称的两个区域.

    如果函数满足下列条件：（i）将保角映射到；（ii）在上连续，将单叶映射到.那末存在一个函数具有性质：

    1^o  把区域保角映射到区域.

    2^o   在内，.

    3^o  将区域内关于对称的两点映射到区域内关于对称的两点.

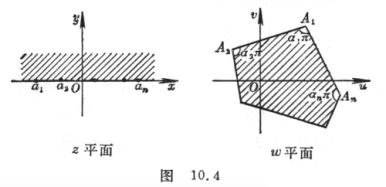
    [多边形映射]  多边形映射是把半平面映射到一个多边形的映射.

    设平面实轴上有个点，平面上一边形，顶点是，在点处的顶角是，那末施瓦兹-克里斯托弗尔积分

                   

是三个常数）把平面的上半平面映射到已给边形内部, 平面实轴上的个点分别映射到平面的边形的个顶点（图10.4）.

    如果平面的无穷远点（设）与边形一个顶点（设）对应，那末映射简化成

    例   求矩形映射把平面的上半平面映射到平面上的一个矩形的内部（图10.5）.

   解 首先考虑平面的第一象限映射到矩形内部的右半部分.同时让的原象记为.把这个映射关于轴的正半轴应用对称原理，就有，同时根据施瓦兹-克里斯托弗尔积分，所求的映射就是

由于，所以，又由于.所以

                                                       (1)

即                                                        (2)

    设   常数已知，适当选择矩形的长和宽（即和），使（1）、（2）式中的常数.

这是第一类椭圆积分（第十二章§1，十）.