2、勒贝格积分

    [有界函数的勒贝格积分]  在有界区间内给定一个有界可测的实函数，在（）的变化范围内插入分点：

                                          （1）

并用表示使在内的点x所构成的集，对每个分法（1）的序列，当时，和式趋于唯一的有限极限I，记作

这个量称为在内按勒贝格意义的定积分，又称为勒贝格积分，称在内是可积（在勒贝格意义下，下同）的.

    [无界函数的勒贝格积分]   若在有界区间内是无界可测函数，则勒贝格积分定义如下：

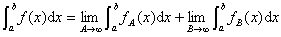
式中

[在无界区间上的勒贝格积分]  若对一切存在，则定义勒贝格积分如下：

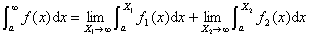
式中         

同样可以定义和.

[在一个点集上的勒贝格积分]  上述有界和无界函数的勒贝格积分的定义可推广到任一个可测集S上的勒贝格积分. 还可推广到n维空间的区域或可测集上的多重勒贝格积分.

[勒贝格积分的存在性与性质]

1^o每个有界可测集函数在任一有界可测集上是可积的，在一可测集S上的可积函数在S的每个子集上都是可积的.

2^o勒贝格积分存在的充分必要条件是：勒贝格积分存在.

3^o在一个测度等于零的集上的勒贝格积分等于零.

4^o设为一组可数的互不相交（即）的可测集，假定在和上的勒贝格积分都存在，则

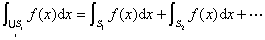
5^o连续性定理  设和一个正的函数在一个可测集S上都是可测的，并且对一切n与S中一切x，不等式

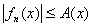
几乎处处成立；又设对S中几乎一切x，使成立，则

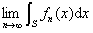
存在，且

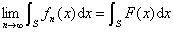
6^o勒贝格基本定理  设S是一个可测集，不一定有界.

若

    (i) 都是S上非负的可测函数；

    (ii)

则