§5   黎曼几何初步

一、   一、 黎曼空间

[黎曼空间及其度量张量]  若n维空间Rⁿ中有一组函数g_ij ( xⁱ )=g_ji ( xⁱ )，使得两邻点xⁱ，

xⁱ＋d xⁱ之间的距离ds由一个正定二次型

ds² = g_ij ( x )dxⁱdx^j

决定，则称空间Rⁿ为黎曼空间，记作Vⁿ.称黎曼空间Vⁿ中的几何学为黎曼几何.二次型 ds²称为Vⁿ的线素.定义曲线弧长的微分为

而任一曲线xⁱ =xⁱ(t)的弧长为积分

    因为在坐标变换

下，ds²为一个不变量，所以

这表明g_ij ( x )为一个二阶协变张量的分量，它称为黎曼空间Vⁿ的度量张量或基本张量.

    [矢量的长度·两矢量的标量积和夹角·伴随张量]   在黎曼空间中关于标量(场)、矢量(场)、张量(场)等的定义类似前面各节，它们的运算法则也相仿.

    设是一个逆变矢量，则其长度的平方为

g_ijaⁱa^j

    设与是两个逆变矢量，则其标量积为

g_ijaⁱb^j

这两矢量夹角的余弦为

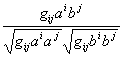
    设

g_ijaⁱ =a_j , g_ijbⁱ =b_j

则与都是协变矢量，它们的长度与标量积分别为

g_ijaⁱ a^j=a_ja^j , g_ijaⁱb^j =a_jb^j

    张量的伴随张量为

，

式中g^lj满足等式

式中为克罗内克尔符号.

    [黎曼联络与克里斯托弗尔符号]  在黎曼空间中总可以用唯一的方式确定联络，满足条件：

    (i)  仿射联络是无挠率的，即

    (ii)  仿射联络所产生的平行移动保持矢量的长度不变.

    这种称为黎曼联络或勒维－奇维塔联络.

    根据上述两个条件可以得出

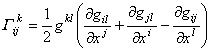
如果记

则有

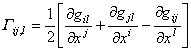
有时用下面的记号：

和

它们分别称为第一类和第二类克里斯托弗尔三指标符号.

    此外，还有等式

或

还要指出，§4中关于协变微分法的一切结果，对黎曼联络都成立.