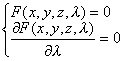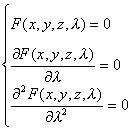§11 可展曲面
[单参数曲面族的包络面]
|
定 义 |
方 程 |
|
包络面 与曲面族Sλ的所有曲面相切的曲面称为Sλ的包络面. 脊 线 族Sλ中两个临近曲面的交线的极限位置称为Sλ的特征线,特征线的包络(如果存在)称为族Sλ的脊线 |
|
[单参数平面族的包络面]
|
定 义 与 性 质 |
方 程 与 图 形 |
|
|
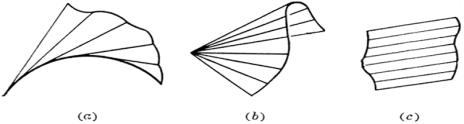
可展曲面 单参数平面族的包络面称为族的可展曲面.包络面是空间曲线的切线所构成的曲面、锥面或柱面(图(a),(b),(c)) |
单参数平面族方程为 ra(λ)+p(λ)=0(λ为参数) 其包络面满足方程组 式中 |
|
|
|
||
|
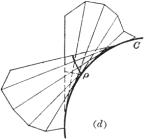
脊 线 平面族中两个邻近平面的交线的极限位置称为族的特征线,特征线的包络(如果存在)称为族的脊线,它把包络面分为两叶,以脊线作为曲面的“尖锐的梭边”(图(d)) |
脊线满足方程组 |
|
|
|
||
|
|
|
|
例 一条空间曲线C的法面的包络面称为C的配极可展曲面,它是曲率轴(即通过曲率中心并平行于副法线)的轨迹.脊线的方程为
式中![]() 为曲线C的曲率半径,
为曲线C的曲率半径,![]() 为曲线C的挠率半径,
为曲线C的挠率半径,![]()
![]()
[空间曲线的渐开线与渐屈线]
|
定义与性质 |
方程与图形 |
|
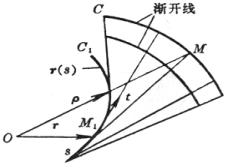
渐开线 在一条空间曲线r(s)的可展曲面上与曲线r(s)正交的曲线称为r(s)的渐开线. 沿r(s)的切线上两条渐开线之间的距离保持不变(右图) |
|
|
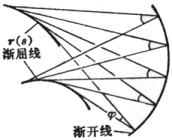
渐屈线 空间曲线r(s)对它的渐开线而言就是渐屈线,也就是渐开线的一族法线包络. 渐屈线C1的一点M1落在C的对应点M的曲率轴上.(上页下图) 如果这族法线组成可展曲面时,则在法面上旋转一个定角,所得到的法线仍然组成一个可展曲面(右图) |
式中为曲率半径,为渐屈线的切线与主法线的交角 |