§9 空间曲线
一、 一、 曲线的基本概念与公式
[曲线的方程与正向]
|
曲 线 方 程 的 形 式 |
曲 线 的 正 向 |
|
交面式 参数式 (t为任意参数,s为曲线的弧长) 矢量式r = r ( t )或r = r ( s ) (r (t) = x (t) i + y (t) j + z (t) k, t, s同上) |
t(或s)增加时,曲线上一点运动的方向 |
|
图 7.18 |
[活动标架的三个单位矢量]
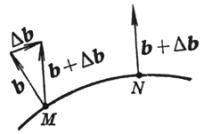
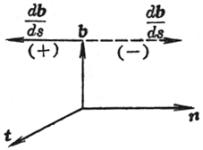
t为单位切线矢量,方向与曲线的正向一致;n为单位主法线矢量,它指向曲线的凹方;b为单位副法线矢量,b=t![]() n.t,n,b构成右手系(图7.18).这三个矢量称为曲线在点M的活动标架(或叫动标三面形、伴随三面形,也叫活动标形).
n.t,n,b构成右手系(图7.18).这三个矢量称为曲线在点M的活动标架(或叫动标三面形、伴随三面形,也叫活动标形).
[活动标架所在直线和平面的方程] 设M为(x0,y0,z0)(图7.18).
1° 切线 过曲线上两点N,M的直线NM,当N![]() M时的极限位置.其方程为
M时的极限位置.其方程为
参数式![]() (以t为参数)
(以t为参数)
式中![]() 表示
表示![]() 在点M(x0,y0,z0)处的值,等等.参数t可以取为弧长s,这时用
在点M(x0,y0,z0)处的值,等等.参数t可以取为弧长s,这时用![]() 表示
表示![]() ,等等.
,等等.
矢量式 r=r0+![]() (以t为参数)
(以t为参数)
式中![]() 表示
表示![]() 在点M(x0,y0,z0)处的值,
在点M(x0,y0,z0)处的值,![]() 为另一个参数.
为另一个参数.
交面式
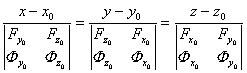
式中![]() 表示
表示![]() 在M点的值,等等.
在M点的值,等等.
2° 法面 与切线垂直的平面(通过M的法面上一切直线都称为曲线在M的法线).其方程为
参数式 ![]() (x-x0)+
(x-x0)+![]() (y-y0)+
(y-y0)+![]() (z-z0)=0(以t为参数)
(z-z0)=0(以t为参数)
式中也可取弧长s为参数.
矢量式
(r-r0)![]() =0(以t为参数)
=0(以t为参数)
交面式

3° 密切面 通过曲线上三点M,P,N作一平面,当![]() 时,平面的极限位置(切线在密切面上).其方程为
时,平面的极限位置(切线在密切面上).其方程为
参数式
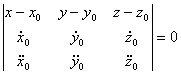 (以t为参数)
(以t为参数)
式中![]() 表示
表示![]() 在M点的值,等等,参数t也可取为弧长s.
在M点的值,等等,参数t也可取为弧长s.
矢量式 ((r-r0)![]() )=0(以t为参数)
)=0(以t为参数)
4° 主法线 法面与密切面的交线.其方程为
参数式  (以t为参数)
(以t为参数)
式中
l= , m=
, m=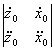 , n=
, n=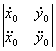
![]() (以s为参数)
(以s为参数)
![]() 表示
表示![]() 在点M的值,等等.
在点M的值,等等.
矢量式 r=r0+![]() (以t为参数)
(以t为参数)
r=r0+![]() (以s为参数)
(以s为参数)
式中![]() 为另一个参数.
为另一个参数.
5° 副法线 垂直于密切面的直线.其方程为
参数式
![]() (以t为参数)
(以t为参数)
式中l,m,n如(1)式定义.
矢量式
r0=r0+![]() (以t为参数)
(以t为参数)
6° 从切面 通过切线与副法线的平面.其方程为
参数式 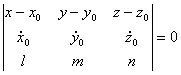 (以t为参数)
(以t为参数)
![]() (以s为参数)
(以s为参数)
矢量式
![]() (以t为参数)
(以t为参数)
![]() (以s为参数)
(以s为参数)
[曲率与挠率的定义与公式]
|
公 式 与 意 义 |
图 形 |
|
曲率
曲率半径
k表示包含点M的部分曲线偏离直线的程度,也是切线方向对于弧长的转动率 |
|
|
挠率
挠率半径
挠率 |
(a)
(b) |
表中![]() 分别表示t,b对s的导数.
分别表示t,b对s的导数.
[曲率与挠率的计算公式]
1° 曲率
参数式
k=![]() (以t为参数)
(以t为参数)
k=![]() (以s为参数)
(以s为参数)
矢量式
k=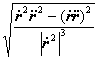 或
或![]() (以t为参数)
(以t为参数)
k=![]() (以s为参数)
(以s为参数)
2° 挠率的绝对值
参数式
 (以t为参数)
(以t为参数)
 (以s为参数)
(以s为参数)
矢量式
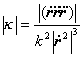 或
或![]() (以t为参数)
(以t为参数)
![]() (以s为参数)
(以s为参数)
式中s为弧长,t为任意参数,“¢”表示对s求导,“×” 表示对t求导.
[雪列-弗莱纳公式(或基本公式)]
![]() ,
, ![]() ,
, ![]()
式中t,n,b为活动标架的三个基本单位矢量,![]() 为曲率半径,
为曲率半径,![]() 为挠率半径.这组公式的特点就是基本矢量t,n,b关于弧长s的导数可以用t,n,b的线性组合来表达,它的系数组成一个反对称方阵:
为挠率半径.这组公式的特点就是基本矢量t,n,b关于弧长s的导数可以用t,n,b的线性组合来表达,它的系数组成一个反对称方阵:

这组公式与![]() =t合并起来描述了点M在曲线上移动时活动标架的运动规律.
=t合并起来描述了点M在曲线上移动时活动标架的运动规律.
把活动标架看作一个刚体,就是当M沿曲线移动时,M的活动标架好象刚体那样绕M转动.这时把s看作时间,则根据运动学的原理可以得出活动标架的瞬时转动速度的表达式为
![]()
这表明转动矢量落在从法面上.这个瞬时转动矢量称为达布矢量.它仅分解为两个矢量![]() t和
t和![]() b,因此活动标架的瞬时转动可以看作两个转动之和.一个转动对应于
b,因此活动标架的瞬时转动可以看作两个转动之和.一个转动对应于![]() t,按转动速度的定义,它绕着方向为
t,按转动速度的定义,它绕着方向为![]() t的轴转动;另一个绕着方向为
t的轴转动;另一个绕着方向为![]() b的轴转动.因此得到曲率与挠率的运动学意义:
b的轴转动.因此得到曲率与挠率的运动学意义:
曲线的曲率等于活动标架绕着副法线的转动支量,挠率等于绕着切线的转动支量.
最后,由![]() 可以验证,空间曲线的雪列-弗莱纳公式就是
可以验证,空间曲线的雪列-弗莱纳公式就是

这就是雪列-弗莱纳公式的运动学意义.
[基本定理与自然方程] 在一闭区间a![]() s
s![]() b上给定任意两个连续函数k(s)和
b上给定任意两个连续函数k(s)和![]() (s),其中k(s)>0,则除了空间的位置差别外,唯一地存在一条空间曲线,它以s为弧长,可k(s)为曲率,
(s),其中k(s)>0,则除了空间的位置差别外,唯一地存在一条空间曲线,它以s为弧长,可k(s)为曲率,![]() (s)为挠率.
(s)为挠率.
方程组
k=k(s), ![]() =
=![]() (s)
(s)
称为空间曲线的自然方程.