§ 5 二次曲线
一、圆
[圆的方程、圆心与半径]
|
方 程 与 图 形 |
圆 心 与 半 径 |
|
|
x2 + y2 = R2 或 (参数方程,t为动径OM与x轴正方向的夹角) |
|
圆心 G(0,0) 半径 r = R
|
|
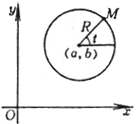
(x - a)2+(y - b)2 = R2 或 (参数方程,t为动径OM与x轴正方向的夹角) |
|
圆心 G(a, b) 半径 r = R
|
|
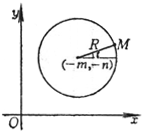
x2 +y2 +2mx + 2ny + q = 0 m2 + n2 > q r2+2r(mcost + nsint) + q = 0 (极坐标方程) |
|
圆心 G(-m,- n) 半径
|
|
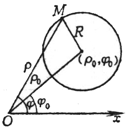
r2-2rr0cos(j- j0)+r02 = R2 (极坐标方程) |
|
圆心 G(r0,j0) 半径 r = R
|
|
x2 + y2 = 2Rx 或 r = 2Rcosj (极坐标方程) |
|
圆心 G(R, 0) 半径 r = R |
|
x2 + y2 = 2Ry 或 r = 2Rsinj (极坐标方程) |
|
圆心 G(0,R) 半径 r = R |
[圆的切线]
圆 x2 + y2 = R2 上一点M(x0, y0)的切线方程为
x0x + y0y = R2
圆 x2 + y2 + 2mx + 2ny + q = 0 上一点M(x0, y0)的切线方程为
x0x + y0y + m(x + x0) + n(y + y0) + q = 0
[两个圆的交角、圆束与根轴]
|
方 程 与 图 形 |
公 式 与 说 明 |
|
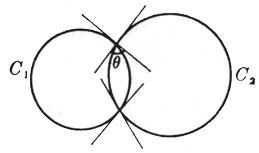
两个圆的交角 C1 x2 +y2 +2m1x +2n1y +q1 = 0 C2 x2 +y2 +2m2x +2n2y +q2 = 0 两个圆的交角是指它们在交点的两条切线的夹角
|
式中q 表示两个圆C1和C2的交角,因为公式中不包含交点的坐标,所以在两交点的两交角必相等. 两个圆C1和C2正交条件为 2m1m2 + 2n1n2 - q1 - q2 = 0 |
|
圆束× 两个圆的根轴
或 (l+1)(x2+y2) +2(m1+l m2)x +(n1+ln2)y + (q1 +lq2) = 0 根轴方程为 2(m1 - m2)x + 2(n1 - n2)y + (q1 - q2) = 0
|
对l
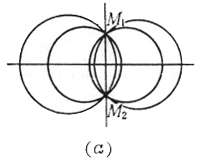
(l ¹ -1)的一个确定值, (a)如果C1和C2 相交于两点M1,M2,则束中一切圆都通过两交点M1,M2,它们的根轴就是它们的公共弦.这时圆束称为共轴圆系(图(a)). (b)如果C1和C2切于一点M,则束中一切圆都在一点M相切,根轴就是在点M的公切线(图(b)). (c)如果C1和C2不相交,则束中一切圆都不相交,根轴也与圆束中一切圆都不相交(图(c)). 从点P作两个圆C1和C2的切线,具有相等切线长的点P的轨迹就是根轴.两个同心圆的根轴是从公共圆心到无穷远处的直线.三个圆中每对圆的根轴(共三个)交于一点,它称为根心.若三个圆心共线,则其根心在无穷远处. |
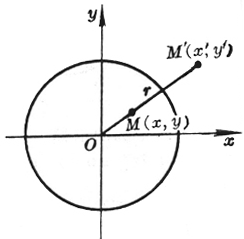
[反演] 设C为一定圆,O为圆心,r为半径(图7.1),对平面上任一点M,有一点M¢ 与它对应.使得满足下列两个条件:
(i)O, M, M¢ 共线,
(ii)OM× OM¢ = r2,
这种点M¢ 称为点M关于定圆C的反演点,C称为反演圆,O称为反演中心,r称为反演半径.
由于M和M¢ 的关系是对称的,所以M也是M¢ 的反演点.因r2 > 0,所以M和M¢ 都在O的同侧.M和M¢ 之间的对应称为关于定圆C的反演.
取O为原点,则一切反演点M(x, y)和M¢ (x¢ ,y¢ )的对应方程为
![]()
反演具有性质:
1° 不通过反演中心的一条直线变为通过反演中心的一个圆.
2° 通过反演中心的圆变为不通过反演中心的直线.
3° 通过反演中心的一条直线变为它自己.
4° 不通过反演中心的圆变为不通过反演中心的圆.
5° 反演圆变为它自己.
6° 与反演圆正交的圆变为它自己,其逆也真.
7° 如果两条曲线C1,C2交于一点M,则经过反演后的曲线C1¢ , C2¢ 必交于M的反演点M¢ .
8° 如果两条曲线C1, C2在一点M相切,则经过反演后的曲线C1¢ , C2¢ 必在M的反演点M¢ 相切.
9° 两条曲线的交角在反演下是不变的.由此可见,反演是一个保角变换.