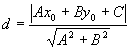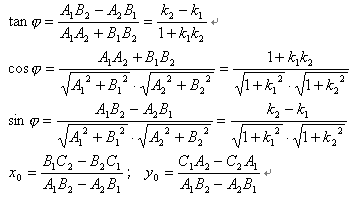二、平面上点与直线的相互关系

方 程 与 图 形	计 算 公 式 与 说 明
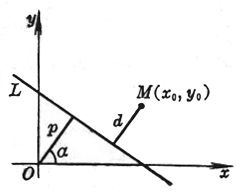
[点线的距离] 法线式 一般式	d法= 式中d为点M(x0, y0)到直线L的距离
[二直线的夹角] L1           A1x + B1y + C1 = 0 斜率为k1 L2           A2x + B2y + C2= 0 斜率为k2 为二直线的夹角（从L1到L2为逆时针时为正），为二直线的交点	特别， 当(或)时，L1//L2; 当时，L1与L2重合； 当A1A2+B1B2 = 0 (或1 + k1k2 = 0)时，L1⊥L2
方 程 与 图 形	计 算 公 式 与 说 明
[直线束× 三直线共点的条件] Ll (A1x + B1y + C1) + l (A2x + B2y + C2) = 0,       (l 为参数，-¥ < l < ¥ )	对l 的一个确定值，Ll 表示一条通过二直线(L1和L2)的交点G的直线，当l 取一切值时，Ll 所表示的通过G的直线的全体称为直线束，G称为直线束的顶点(或中心). 设L3为A3x + B3y + C3 = 0，则三条直线L1, L2, L3共点的条件为行列式 如果二直线方程以法线式给定，则|l |为直线Ll 上任一点到二给定直线之间的距离之比，对应与 l = 1和 l = -1的直线为给定二直线夹角的平分线