三、n维空间中凸体体积公式
n维空间的点的坐标为(![]() ).所谓n维空间中的凸体
).所谓n维空间中的凸体![]() ,是指
,是指![]() 中任意两点A和B的连线仍在
中任意两点A和B的连线仍在![]() 中,即设A=
中,即设A=![]() B=
B=![]() ,若A,B∈
,若A,B∈![]() ,则点
,则点![]() .其中
.其中
![]() , i=1,2,…,n
, i=1,2,…,n
下面列出几种凸体体积的计算公式.
[单纯形] 已知n维空间中的n+1个点![]() ,包含这n+1个点的最小凸体称为由
,包含这n+1个点的最小凸体称为由![]() 张成的单纯形,记作
张成的单纯形,记作![]() ,若设
,若设![]() 的n个坐标为
的n个坐标为
(![]() ) i=1,2,…,n+1
) i=1,2,…,n+1
则单纯形![]() 的体积
的体积
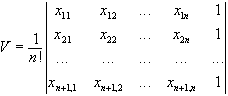
n=2时为三角形,n=3时为四面体.
[超立方体]
![]() :
|
:
|![]() |≤
|≤![]() ,
i=1,2,…,n
,
i=1,2,…,n
V=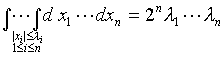
[广义八面体]
1°![]() 1:
1:![]() ≤r,
≤r, ![]() >0, i=1,2,…,n
>0, i=1,2,…,n
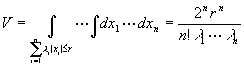
2°![]() 2:
2:![]() ≤r,
≤r, ![]() >0,
>0, ![]() >0,i=1,2,…,n-1
>0,i=1,2,…,n-1
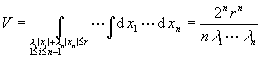
[n维球体]
![]() :
:![]()
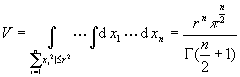
[凸体的线形变换] 设有线性变换
![]() =
=![]() , i=1,2,…,n
, i=1,2,…,n
J=det(dij)≠0
将凸体R映成![]() ,则
,则![]() 的体积为
的体积为
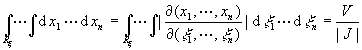
这里![]()
![]() 为该线性变换的雅可比式.
为该线性变换的雅可比式.