2. 三重积分

       [直角坐标下的三重积分]  假设有界区域V由下列不等式

              a≤x≤b, ≤y≤, ≤z≤

 确定，其中,,,都是连续函数，且函数f(x,y,z)在V上是连续的，则函数f(x,y,z)在有界区域V上的三重积分

             

   有时采用下面公式计算：

             

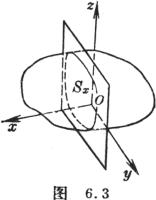
式中是用平行于Oyz的平面截区域V所得的截断面(图6.3).

       例 设V表示在第一卦限中由曲面和坐标平面所围成的封闭区域，则当一切常数都是正的时候，有

               

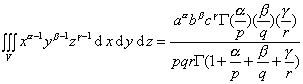
这种类型的积分称为狄利克莱积分，它在计算重积分时经常用到.

             

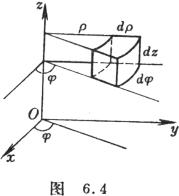
       [圆柱坐标下的三重积分]  (图6.4)

        

                                   （一般地，0≤≤2π)

式中V为直角坐标中的有界区域，V'是区域V在圆柱坐标系中的表达式.

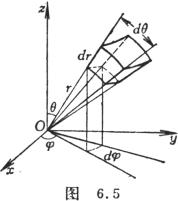
       [球面坐标下的三重积分]  (图6.5)

                         （一般地，0≤≤2π,0≤θ≤π)

式中V'是区域V在球面坐标系中的表达式.

       [三重积分的变量替换(雅可比式)] 若连续可微函数

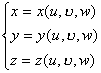
把Oxyz空间的有界三维闭区域双方单值地映射到O'uw空间的闭区域V'，并且当（u, ,w)∈V'时其雅可比式

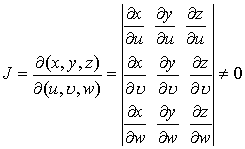
则