4、作图
作函数
y = f(x)
的图形的步骤大致有以下几点:
(1) (1)确定自变量x的改变区间,讨论函数的一些基本性质,如奇偶性、对称性和周期性等;
(2) (2)确定曲线与坐标轴的交点;
(3) (3)确定曲线的顶点(极大点、极小点);
(4) (4)确定曲线的凸部,凹部与拐点;
(5) (5)确定曲线的渐近线;
(6) (6)描点作图.
当然,具体问题要具体分析,以上几点不一定都要讨论.
例 画曲线
y=![]()
(1) (1)x可以在区间(-∞,∞)上改变,不对称,也无奇偶性和周期性.
(2)
(2) 让x=0,得到y=![]() ;让y=0,得到x=3;就是,曲线与坐标轴交于点(0,
;让y=0,得到x=3;就是,曲线与坐标轴交于点(0,![]() ),(3,0) (图5.10).
),(3,0) (图5.10).
(3)
(3) 求出一阶与二阶导数![]() ,
,![]() ,得到顶点(3,0)(极小点)和
,得到顶点(3,0)(极小点)和
(-1,-2)(极大点).
(4)
(4) 二阶导数当x>1时为正,当x<1时为负.因此,在区间(1, ∞)内曲线是凹的,在区间(-∞,1)内曲线是凸的.因为![]() 只当x=1时变号,而x的这个值对应于一条平行于y轴的渐近线,所以没有拐点.
只当x=1时变号,而x的这个值对应于一条平行于y轴的渐近线,所以没有拐点.
(5) (5) 当x=1时,y成为无穷大,于是这曲线有一条渐近线x=1.
再求不平行于y轴的渐近线.
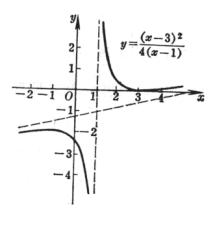
|
图5.10 |
k=![]()
b=![]()
![]()
所以
y=
是一条不平行于y轴的渐近线.
由这些性质描出曲线(图5.10).