4．约束条件为不等式的条件极值

比前面所考虑的更一般的极值问题是求函数

y =f (x)，x = (x₁,x₂,…,x_n)

在m个约束条件

g_k(x)，k =1,2,…,m

下的极值问题，这里的m不必小于n.

[松弛变量法]  对每一约束不等式都引进一非负的松弛函数S_i, 将它变为等式：

=g_i+S_i=0

每一松弛函数S_i仅依赖于一个松弛变量x_n+i,一般取

S_i=

引进松弛函数后就把问题化为约束条件是等式的极值问题，前面的方法就可以应用了.

例3        例3          求函数

y =

在约束条件

x₁

下的极值.

解  约束条件可写为

g₁=1- x₁

利用松弛函数S₁(x₃)可将这个不等式约束化为等式

=g₁+S₁=x₁+=0

利用直接代入法可在函数y中将x₁消去得到

y=4(1+)²+5

这是一个无约束问题.

稳定点是x₂=0,x₃=0,所以x₁=1.由于

D₁==10>0

D₂=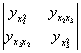==160>0

所以稳定点是修改后的以及原来的函数的极小点，其极小值为4.

[拉格朗日乘数法]  引进松弛函数后，将约束不等式化为等式

=g_k+S_k(x_n+k)=0,      k=1,,m

同等式约束的情形一样，引进新的目标函数

F=y+

这是一个n+2m个变量的无约束问题.稳定点可以由解下列方程组得到

=0，      j=1,,(n+m)

=0,    k=1,,m

以上介绍的多变量函数的极值和条件极值求法中，求稳定点时最后都归结为求实函数方程组

f_I  (x₁,,x_n)=0,  i=1,,n

的一组实根.有时上列方程组的实根不易求得，要求近似根.关于实根的近似计算法可参考第三章，§4.