3. 由方程组所确定的隐函数

对由方程组

                                (1)

所确定的隐函数有下述定理:

[存在定理]  设函数F(x,y,z)及G(x,y,z)在点P₀(x₀,y₀,z₀)的某一邻域R内定义,并且满足下列条件:

(i)   F(x,y,z),G(x,y,z)及其所有偏导数都在R内连续,

(ii)  F(x₀,y₀,z₀)=0,G(x₀,y₀,z₀)=0,            

(iii) 行列式

J(x,y,z)=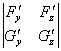

在点P₀(x₀,y₀,z₀)不等于零:J(x₀,y₀,z₀)≠0.

那末在点P₀(x₀,y₀,z₀)的某一邻域

;;)

内有唯一的一组单值函数y=f(x),z=g(x)存在,具有下列性质:

1°  F[x,f(x),g(x)]≡0,G[x,f(x),g(x)]≡0,且f(x₀)=y₀,g(x₀)=z₀,

2°  在区间()内函数f(x),g(x)连续,

3°  在这区间内有连续导数.

[导数的计算]  将y和z看作x的隐函数,将方程组(1)对x微分得

这是关于及的线性方程组,其行列式J≠0,由此可以解出及.

注意,对于由方程组

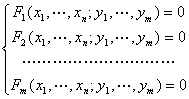
所确定的隐函数有类似的结果.