5．不定式的定值法—洛比达法则

洛比达法则是用来计算，，，，⁰，⁰，等七种不定式的极限的法则*.

[洛比达第一法则（）]  设(i)函数f(x)和g(x)是在区间(a,b]内定义的，(ii) f(x)=0, g(x)=0,(iii)在区间(a,b]内存在有限导数及，而且≠0，(iv)存在极限(有穷或无穷)

=K

那末

                                                    ==K

若又是型不定式，可再用上法求极限.

[洛比达第二法则（）]设(i)函数f(x)和g(x)是在区间(a,b]内定义的，(ii) f(x)=, g(x)=,(iii)在区间(a,b]内存在有限导数及，而且≠0，（iv）存在极限（有穷或无穷）

=K

那末

==K

若又是型不定式，可再用上法求极限。

[其他类型不定式（，，，⁰，⁰）]

(1) 对型的不定式，可先把它变成型或型，然后再应用洛比达法则。设

f(x)=0, g(x)=

如果要计算f(x)·g(x),那末可以进行变形

f(x)·g(x)==

其中的第二式在时是型不定式，第三式是型不定式.

(2) 型的不定式也能变成型或型，如果要计算 [f(x)-g(x)],这里

f(x)=+, g(x)=+

那末可以进行下面的变形，把它变成型不定式：

f(x)-g(x)=

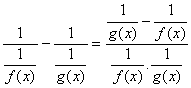
(3) 对于，⁰，⁰型的不定式，可以预先把这些表达式取对数.

设y=[f(x)]^g(x),则y=g(x)f(x). y的极限就是型的不定式.假如用上述任一方法能求出y，比如它等于k（或+，或-），那末y就等于e^k(或，或0).