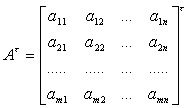
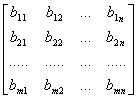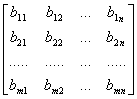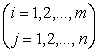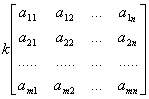§2 矩阵的运算
一、 一、 矩阵的相等、加、减、数乘、乘法、转置与共轭
|
运算及其规则 |
性质与说明 |
|
[相等]
当且仅当 |
相等矩阵必须具有相同行数与相同列数. 两矩阵相等,指各对应位置的元素分别相等. |
|
[加减]
= 其中 |
同类型的矩阵才能相加减(各对应位置的元素相加减). A+B=B+A (交换律) (A+B)+C=A+(B+C) (结合律) |
|
[数乘]
|
数乘矩阵时,将数乘到矩阵的每个元素上. kA=Ak k(A+B)=kA+kB (k+l)A=kA+lA k(lA)=(kl)A (k,l为任意两个复数) |
|
[乘法] 若 A=(aij)为m´n矩阵 B=(bij)为n´s矩阵,则 AB=(aij) (bij)=(cij)=C 式中C为m´s矩阵,且 cij= 运算及其规则 |
乘积的元素cij,等于左矩阵的第i行与右矩阵的第j列对应元素相乘之后相加. 左矩阵的列数必须等于右矩阵的行数. (AB)C=A(BC)
(结合律) k(AB)=(kA)B=A(kB) (k是任意复数) [注]AB=BA一般情况下不成立,即无交换律. 性质与说明 |
|
[转置] 把m´n矩阵A=(aij)的列同行互换后所得到的n´m矩阵称为A的转置矩阵,记作
= |
(A+B)t=At+Bt (kA)t=kAt(k为任意复数) (AB)t=BtAt(反序定律) (A1A2...As)t= (Ak)t=(At)k (k为整数) |
|
[共轭] 把矩阵A=(aij)的所有元素换成它们的共轭复数后所得到的矩阵称为A的共轭矩阵,记作
|
|