九、下降法

对任意实系数超越方程组

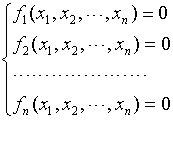(1)

定义目标函数

F(x₁,x₂,L ,x_n)=

如果F(x₁,x₂,L,x_n)<e （e为在一定精确度下给定的适当小的正数），则认为x₁,x₂,L ,x_n为方程组（1）的解.

       具体计算步骤如下：

（1）任取一组初始值x₁⁽⁰⁾,x₂⁽⁰⁾,L,x_n⁽⁰⁾（全不为零），设已按照下述过程计算到第m步得到一组值：x₁^(m),x₂^(m),L ,x_n^(m)

（2）计算

F_m=F(x₁^(m),x₂^(m),L ,x_n^(m))

（3）若F_m<e ，则x₁^(m),x₂^(m),L ,x_n^(m)是所求的解，否则计算n个偏导数：

[F(x₁^(m),x₂^(m),L,x_i^(m)+H_i,L,x_n^(m))-F（x₁^(m),x₂^(m),L ,x_n^(m)）]

H_i=wx_i^(m)       i=1,2,L ,n

（4）计算

x_i^(m+1)= x_i^(m),  i=1,2,L,n

式中

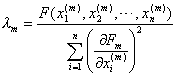
得到一组{x_i^(m+1)}，再重复（2），（3）,（4）的计算.