§4  实根的近似计算

       设f(x)为已知连续函数，ξ是方程

f(x)=0

的根，这里方程可以是一般方程（代数方程或超越方程）.在实际问题中都给出了根的范围，例如代数方程

f(x)=a₀xⁿ+a₁x^n－1+L+a_n－1x+a_n=0

的根ξ的范围是

|ξ|£1+max{|a₁|,|a₂|,L,|a_n|}

因此可以假定方程在区间(a,b)内只有一个根（若有两个根，则将区间的一个端点换为使(x)=0的点）.并由函数的连续性可知，一般来说，在根的附近f(x)是异号的（当(ξ)=0或除外），所以在下面介绍的各种近似计算中，都假定f(a)和f(b)异号.

一、秦九韶法*

秦九韶法基本上是通过逐次试验求根的近似值的方法，试验次数愈多，所得近似值愈接近根的真值.系统地继续这一过程，直至达到预定的有效数字的位数.现举例具体说明这个方法.

例   求方程

                     f(x)=                              (1)

的根到五位有效数字.

应用笛卡尔符号法则可知这个方程有一个正根.由于f(1)＝－11，f(2)＝14，这个正根在(1,2)之间.

现在应用秦九韶法求这个方程的近似根.先设，这里表示1到所求根的距离.应用多项式的泰勒公式(秦九韶法,见§2,一)，得到关于的方程

                                                (2)

其算式为

                    

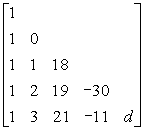
   现在求纯小数的近似值，由于纯小数的三次方或二次方的值更小，可暂舍去方程(2)的头两项而来计算21－11＝0，即＝0.5238….但舍去的两项是正的，这个值显得太大.当＝0.500时，方程(2)的左边各项的和是仍是正数(0.375)，而当＝0.400时，方程(2) 的左边各项的和是负数(－2.056).因此，设,即，再应用多项式的泰勒公式，得到关于h的方程

                                               (3)

其算式为

                    

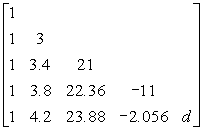
现在求小数h的近似值，舍去头两项，求得h＝0.08609….因舍去两个正量，所得的h太大，所以设h＝0.08,即.应用上述方法得到关于的方程

                                        (4)

同上面一样，从方程(4)的后两项求得设,即

* 我国古代数学家秦九韶在他所著的<<数书九章>>(1247)，给出一个求代数方程的根近似值

  的方法，这个方法一般书上都称为和纳法.实际上和纳在1819年才提出这个方法，比秦九

  韶晚五百多年.

得到关于的方程

                                  (5)

从后两项求出的近似值=0.0008…,因舍去的都是正量，所以方程(5)的根在0.0008和0.00081之间.

现在把(2),(3),(4),(5),的各个近似值0.4,0.08,0.004,0.0008相加得总和0.4848,然后加到第一次近似值1上，所以方程(1)的根在1.4848与1.48481之间，取五位有效数字为1.4848.

用秦九韶法还能求负的近似值.想求f(x)＝0的一切负实根，可先求 f(－x)的正实根，然后改变符号，即得负实根.