4.四次方程

       [ax⁴+cx²+e=0] 方程

ax⁴+cx²+e=0

中，设y=x²，则化为二次方程

ay²+cy+e=0

可解出四个根为

                                   x_1,2,3,4=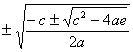

[ax⁴+bx³+cx²+bx+a=0] 方程

ax⁴+bx³+cx²+bx+a=0

中，设y=x+，则化为二次方程，可解出四个根为

x_1,2,3,4=, y=

[x⁴+bx³+cx²+dx+e=0]    一般四次方程

ax⁴+bx³+cx²+dx+e=0

都可化为首项系数为1的四次方程，而方程

x⁴+bx³+cx²+dx+e=0

的四个根与下面两个方程的四个根完全相同：

x²+(b+)(y+)=0

x²+(b－)(y－)=0

式中y是三次方程

8y³-4cy²+(2bd-8e)y+e(4c-b²)-d²=0

的任一实根.