3.三次方程
[x3－1=0] 方程 x3－1=0
的三个根为
x1=1, x2=ω=
, x3=ω2=
(i2=－1) (1)
[x3+px+q=0(卡尔丹公式)] 方程
x3+px+q=0
的三个根为
x1=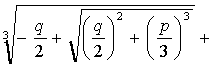 
x2=ω 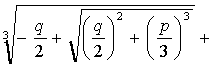ω2 (2)
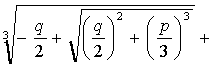x3=ω2 ω
式中ω,ω2同(1).这叫做卡尔丹公式.
根与系数的关系为
x1+x2+x3=0,
x1x2x3=－q
判别式为
=
>0时，有一个实根和两个复根；=0时，有三个实根，当p=q=0时，有一个三重零根；当
时，三个实根中有两个相等；<0时，有三个不等的实根.
三个根的三角函数表达式（仅当p<0时）为
x1=2 
cosθ
x2=2 
cos(θ+120°)
x3=2 cos(θ+240°)
式中
r=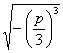
, θ=
arc cos
[ax3+bx2+cx+d=0] 一般三次方程
ax3+bx2+cx+d=0 
上式除以a，并设
x=y
则化为如下的形式
y3+py+q=0
可按（2）的情形处理，解出y1，y2，y3，则一般三次方程的三个根为
x1=y1 ， x2=y2
，
x3=y3
三个根与系数的关系为
x1+x2+x3=
, 
, x1x2x3=