图形

面积S、几何重心G与转动惯量*J

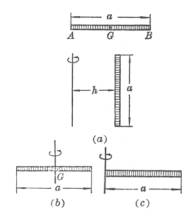
[直线段]

长度   L=a

重心   GA=GB=

转动惯量

(a)    (a)转轴平行于细杆，到细杆距离

  为h(图(a))

(b)    (b)转轴通过细杆重心G,且与细杆

  垂直(图(b))

(c) (c) 转轴通过细杆的一个端点,且与细

  杆垂直(图(c ))

图形

面积S、几何重心G与转动惯量J

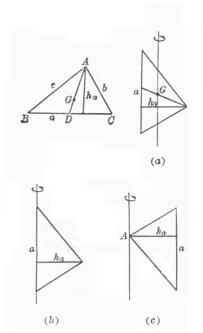
[任意三角形]

   a,b,c为三边,为a边上的高

[等腰三角形]

b为两腰,a为底边,为a边上高

重心     

转动惯量

(a)转轴通过重心G,且与a边平行

    (图(a))

(b)转轴与三角形一边a重合(图(b))

(c)转轴通过三角形一顶点A,且平行于a边(图(c ))

重心      

转动惯量

  转轴与底边上的高重合

   当a=b时

图形

面积S、几何重心G与转动惯量J

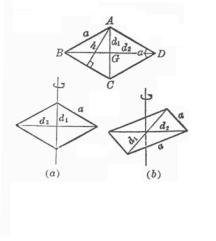
[矩形]

   a,b为邻边,d为对角线, 为对角线的夹角

[菱形]

a为边长,为顶角,为两对角线

面积    

重心 G在对角线的交点上,即

转动惯量

(a)转轴通过矩形中心,且垂直于矩形所在平面(图(a))

(b)转轴通过矩形中心,且与矩形的b边平行(图(b))

(c)转轴与矩形的b边重合(图(c))

面积  

重心G在对角线交点上,即

转动惯量

(a)转轴与对角线重合(图(a))

(b)转轴通过重心G且垂直于图形所在平面(图(b))

图形

面积S、几何重心G与转动惯量J

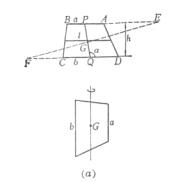
[平行四边形]

a,b为邻边,h为对边距,为顶角,为两对角线,为两对角线夹角

[梯形]

a,b为上下底,h为高,l为两腰中点连线

[任意四边形]

a,b,c,d为四边长,为两对角线,为两对角线夹角

面积  

重心   G在对角线交点上

面积  

重心  

转动惯量

转轴通过重心,且平行于上下底

(图(a))

当a=b时(平行四边形)

面积 

    或