4. 某些重要不等式
[算术平均值与几何平均值不等式]
1o 几个数的算术平均值的绝对值不超过这些数的均方根,即
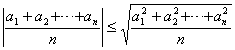
等号只当![]() 时成立.
时成立.
2o 设a1, a2, L , an均为正数,则它们的几何平均值不超过算术平均值,即
![]()
等号只当![]() 时成立.
时成立.
3o 对n个正数a1, a2, L , an的加权平均值![]() ,有
,有
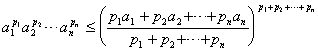
等号只当a1=a2=L =an时成立.
4o 设a1, a2, L , an为正数,又![]() ,则有
,则有

[柯西不等式] 设ai, bi(i=1, 2, L , n)为任意实数,则
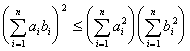
等号只当![]() 时成立.这个不等式表明一个角(取实数值)的余弦值总是小于1的,或者说二矢量内积小于二矢量长度之积.
时成立.这个不等式表明一个角(取实数值)的余弦值总是小于1的,或者说二矢量内积小于二矢量长度之积.
[赫尔德不等式]
1o 设ai, bi, L , li(i=1, 2, L , n)为正数,又a , b , L , l 为正数,且a +b +L +l =1,则
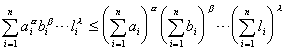
等号只当![]() 时成立.
时成立.
2o 设ai, bi (i=1, 2, L , n)为正数,又k>0, k¹ 1, ![]() 与k共轭,即
与k共轭,即![]() ,或
,或![]() ,则
,则
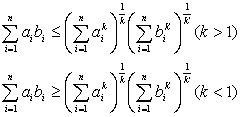
等号只当![]() 时成立.
时成立.
[闵可夫斯基不等式] 设ai, bi>0 (i=1, 2, L , n),又r>0, r¹ 1, 则
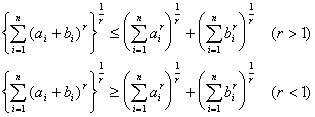
等号只当![]() 时成立.当r=2时,此不等式也称为三角形不等式,它表明三角形两边之和大于第三边.
时成立.当r=2时,此不等式也称为三角形不等式,它表明三角形两边之和大于第三边.
[契贝谢夫不等式] 设ai>0, bi>0 (i=1, 2, L , n).若a1£ a2£ L £ an, 且b1£ b2£ L £ bn, 或a1³ a2³ L ³ an, 且b1³ b2³ L ³ bn, 则
![]()
若a1£ a2£ L £ an而b1³ b2³ L ³ bn,则
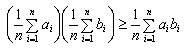
[詹生不等式] 设ai>0 (i=1, 2, L , n),且0<r£ s,则
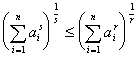
[伯努利不等式] 设a>1,自然数n>1,则
![]()
特别令![]() ,则
,则
![]()